Math Review #1

This is a review of the mathematical concepts we have encountered in this course. It is not extensive. If you feel you need more basic review than this you should visit the following web site: Math for Morons Like Us (I didn't come up with the name)

Geometry

Right Triangles

You'll find that in this course whenever we need to make a measurement of distance that right triangles will be of use. A right triangle is one in which one of the angles is a 90° angle. Recall that the sum of the angles of any triangle is 180°. The relationships between the lengths of the sides of a right triangle and the angles in the triangle are very important. Consider the following figure

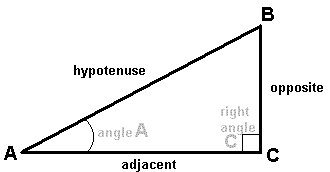
The first thing to remember is that the lengths of the sides of a right triangle are related by the Pythagorean theorem:

(hypotenuse)2 = (opposite)2 + (adjacent)2

This says that the sum of the squares of the "legs" of a triangle (the two sides that meet in the 90° angle) are equal to the square of the hypotenuse (the side that is opposite the 90° angle).

The next thing to remember is the trigonometric functions that relate the ratios of the lengths of the sides of the right triangle to its angles. For angle A in the figure the relations are:

COS(A) = adjacent/hypotenuse
SIN(A) = opposite/hypotenuse
TAN(A) = Cos(A)/SIN(A) = opposite/adjacent

Circles and Spheres

The other shapes that will come up again and again in astronomy are circles and spheres. A circle is the set of points that all lie a given radius, r, away from any specific point in 2-dimensions. A sphere is the same thing but in 3-dimensions.

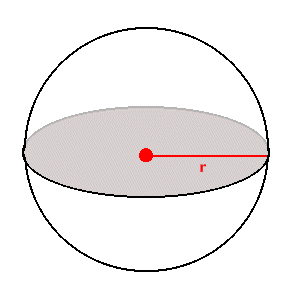
The length around a circle is called the circumference. The ratio of circumference, C, to the diameter, D (D = 2r), is the transcendental number represented by the Greek letter . Hence,

C = 2r

The ratio of the area, A, of a circle to the square of the radius is again . Hence,

A = r2

For a sphere the 3-D equivalent of Circumference is Surface Area, SA. It is given by

SA = 4r2

Finally, the volume, V, of a sphere is given by

V = (4/3)r3

Ellipses

An ellipse is the set of points whose sum of distances to two fixed points (called foci, focus singular) is the same. One way to draw an ellipse is to attach the ends of a string to two fixed points and pull the string tight with a pencil and circle around the points.

The long axis of the ellipse is called the major axis, the short axis is called the minor axis. The distance from the center out to the ellipse along the major axis is called the semimajor axis, usually denoted with the letter a.

Circles are just special ellipses. They are ellipses with both foci at the same point.

Measuring Angles

The ancient Babylonians devised the system of degrees where a circle is divided into 360 equal angles each one having one degree (1°) of arc. Each degree can further be divided into 60 arc minutes (1° = 60'), and each arc minute can be divided into 60 arc seconds (1' = 60"). There is another measure of angles which is a natural result of the connection of angles to circles. It is called the radian. Radians are a pure number and as such have no units. So if ever you see an equation with an angle equal to a unitless quantity it must be measured in radians. There are 2 radians in a circle. Therefore 360° = 2 radians, or 1 radian = 57.3°. In astronomy we typically use the arc second as a measure of angle in the sky. So it's useful to remember that there are 57.3° * 60'/1° * 60"/1' = 206,265" in 1 radian.
Understanding of these simple geometric figures and relations allowed the ancient Greeks to make measurements of the size of the Earth, Moon, Sun and their distances from one another. Review pages 39 - 40 of your text for how these ideas are used with the concept of angular size and distance of an object.

Speed, Time, Distance, and Acceleration

Speed is the amount of distance covered per unit time by a moving object. Another way of saying this is that it's the amount of change in position per unit time. Velocity is the speed + direction of an object. It is what we call a vector quantity. Speed has units of distance/time (i.e., m/s). The relationship between distance, speed, and time is simply
d = vt
Where d, is the distance covered, and t is the time in which it was covered while traveling at a constant speed, v.

Acceleration is the amount of change in velocity per unit time. It has units of distance/time/time (i.e., m/s2). The distance that an object moves in a span of time, t, with a constant acceleration, a, and an initial velocity, v0, is given by

d = v0t + (1/2)at2

Kepler's Laws

Johannes Kepler devised 3 empirical laws of planetary motion which are summed up in the following figure
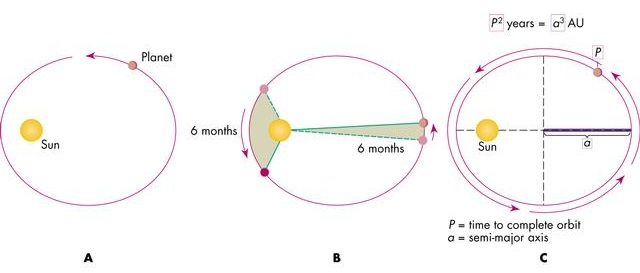
  1. (A): Planets move in elliptical orbits with the Sun at one focus of the ellipse (not the center!).

  2. (B): The orbital speed of a planet varies so that a line joining the Sun and the planet will sweep over equal areas in equal time intervals.

  3. (C): The amount of time a planet takes to orbit once around the Sun is called the period, P, and it's related to the orbit's size, a. The period, P, squared is proportional to the semi-major axis, a, cubed:
    P2 a3

    This says that the farther away a planet is from the Sun it will take a longer time to go around once.

    Newton discovered that the constant of proportionality is dependent on the masses of the objects in orbit, and he wrote Kepler's 3rd law as

    P2 = 42/G(m1 + m2) * a3
    Where G is the universal gravitation constant. If m2 << m1 then we may ignore m2 and then the relation is just
    P2 = 42/Gm1 * a3

    To see an example of the use of this relation see problem #1 of HW #2 and the lecture notes for lecture 5.

Newton's Laws of Motion and Gravity

There are two mathematical laws of Newton's that should be remembered (not necessarily memorized, but understood).

Newton's 2nd Law of motion

This law states that the acceleration,a, of an object is directly proportional to the force, F, applied to it, and the constant of proportionality is the mass, m, of the object.
F = ma
So the equation says if you push harder the object will accelerate more. Also, if an object has more mass you need to push harder to reach the same level of acceleration for an object of lesser mass.

The Universal Law of Gravitation

Newton found that for two bodies with masses, m1 and m2, that are separated by a distance, r, they will experience a force of attraction, F.
F = - Gm1m2/r2
Where G is a constant (G = 6.67 x 10-11 m3*g-1*s-2).

Since F = ma also, then object 1 experiences an acceleration, a1 found by setting the two expressions equal to one another.

- Gm1m2/r2 = m1a1

a1 = - Gm2/r2

Likewise for object 2.

The uses of these formulae are many (e.g., surface gravity). See the lecture notes and HW #2 for examples.

Energy

Energy is a quantity that measures the ability of a system to do work or cause motion. Energy may neither be created nor destroyed in a closed system, but it can change form. There are two forms of mechanical energy
  1. Kinetic Energy: the energy of motion
    for any object with mass, m, and velocity, v, its kinetic energy, KE, is given by
    KE = (1/2)mv2

  2. Potential Energy: the amount of work that can potentially be done
    This has no simple definition, it is defined in a mathematical way. For an object, with mass, m, under the gravitational attraction of another with mass, M, and a distance, r, away the potential energy, PE, is
    PE = - GMm/r
The total mechanical energy, E, of a system is given by the sum of these two energies.
E = KE + PE

E is a constant and so KE and PE can only change in such a way that as one becomes smaller the other becomes larger by the same amount. In other words we can convert potential energy into kinetic energy and vice versa.

Escape Velocity

We came upon the concept of trying to escape from the surface of a gravitating body with mass, M, and radius, R. In order to do this we say that you needed some initial velocity, vesc, that would give you sufficient energy to be unbound (total energy is positive). We could solve for this quantity by setting total energy equal to zero (the minimum requirement needed to escape to infinity).
E = (1/2)mvesc2 - GMm/R = 0
Algebraic manipulation thus gives
vesc = (2GM/R)1/2

(Recall that raising something to the 1/2 power is the same as taking the square root.)

Light and Heat

Wavelength and Frequency

We saw that light behaves like a wave, and waves may be described in terms of their wavelength, frequency, and speed at which they travel. The wavelength, , is the distance from peak to peak (or trough to trough) of the wave. The frequency, , is the number of peaks that pass by a given point per unit time. Clearly, if the speed of a wave, v, increases while keeping the wavelength constant, the frequency will increase. But, if at the same time the wavelength is longer by just the right amount the frequency could stay the same. The three quantities for any wave are related by
= v = c
Where, c, is the specific value that we use for the speed of electromagnetic waves. It is a constant in empty space (a vacuum). c = 3 x 108 m/s

Energy of a Photon

Light can also be thought of as a particle "wave-packet". The particle has no mass, but it does have energy. That energy is given by
E = hc/ = h
Where h is known as Planck's constant (h = 6.63 x 10-34 Joules*seconds, 1 Joule = 1 kg*m2/s2)

So, light with shorter wavelengths has more energy than light with long wavelengths (blue light is more energetic than red light, X-rays are more energetic than microwaves)

Doppler Shift

When an object is in motion and emitting waves the wavefronts in front of the object are compressed (shorter wavelengths, higher frequencies) while the wavefronts behind the object are spread out (longer wavelengths, lower frequencies). For light that means the color (energy) of photons is changed. If the object is moving toward an observer, the observer will see the light emitted by the object blueshifted. If the object is moving away, the observer sees the light redshifted. The amount of redshift or blueshift is proportional to the speed of the object relative to the speed of the waves.

/0 = v/c

Where c is the speed of light, 0 is the wavelength of the light as seen at rest, and is the measured change in wavelength ( - 0).

Blackbody Radiation


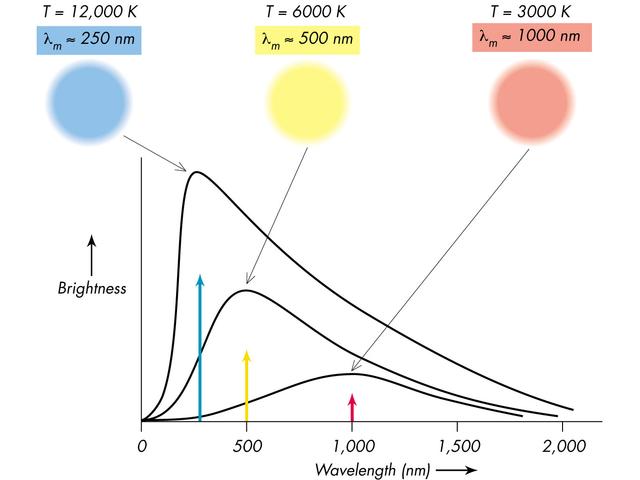
An object with a temperature, T, will radiate energy away with an energy spectrum like that of a theoretical construct called a blackbody (shown in the figure above). The hotter the object the more light energy (photons) it radiates at all wavelengths. But, depending on its temperature it will radiate more photons at certain wavelengths. Thus the color of emitted light from an object can reveal its temperature.

The relationship between temperature, T, and the wavelength at which most of the energy (photons), peak, is emitted is called Wien's Law:

peakT = 2.898 x 10-3 m*K
So, this equation says that as an object gets hotter it radiates more light at shorter wavelengths (higher frequencies, higher energies) and vice versa. Thus an oven burner glowing yellow is hotter than one glowing red.

The relationship between temperature, T, and the total amount of radiation being emitted per unit surface area per unit time, , is called the Stefan-Boltzmann Law:

= T4
Where is the Stefan-Boltzmann constant ( = 5.67 x 10-8 W m-2 K-4). This says that if you double the temperature of an object, then a patch of surface area on that object will emit 16 times more radiation per second.

Telescopes

With telescopes the quantitative aspects were in regard to their light collecting and resolution abilities. We saw that both aspects were dependent on the diameter, D, of the light collecting aperture (mirror or lens).

Light collecting

In order to collect more photons you essentially want a big light bucket that you can allow to collect light for a long time. Since brightness is measured as a flux of photons through a surface area we need to increase the collecting area (which depends on the diameter, A = (D/2)2) and/or the exposure time.

Diffraction Limit

The wave phenomenon of diffraction causes point sources of light (like stars) to be surrounded by rings of diffracted light. The innermost rings must be separated by a minimum angle for us to see two point sources right next to each other as separate entities. The smallest angle, , that a circular aperture, with a diameter D, can resolve for light with wavelength is given by

1.22/D

So this tells us that for any given wavelength we want bigger telescopes to resolve smaller details. It also tells us what size telescope we need to resolve an arbitrary angle at a specific wavelength. (From the surface of the Earth we are limited to how small an angle can be resolved because of the blurring of light as it passes through the atmosphere.) At larger wavelengths we will need larger telescopes to resolve details at the same level as at smaller wavelengths.

In summary. Big Telescopes = Good

Big Telescopes in Space = Even Better

Return to Class Notes Page