Kepler's 3rd Law
(13 points)- Use Kepler's 3rd Law and Neptune's semi-major axis of 30.06 AU to derive Neptune's orbital period in years.
Kepler's 3rd Law states that
P2 Where P is the orbital period and a is the semi-major axis of the elliptical orbit (also the average distance from the Sun). The simplest way to do this problem is by using ratios. We know that for Earth, P = 1 year and a = 1 AU. So let's set up the ratio:
a3 PN2/P 
2 = aN3/a3
Now, solve for the period of Neptune:
PN2 = (aN/a
)3*P2
Now take the square root of both sides:
PN = (aN/a
)3/2*P
Now plug in the values and do some arithmetic
PN = (30.06 AU/1 AU)3/2*1 year = 164.8 years
- The planet Bajor orbits a star 15 times more massive than our Sun. It's orbital period is 268 days. What is the semi-major axis of its orbit in AU? (HINT: Consider Newton's version of Kepler's 3rd Law, and remember to use ratios!)
Newton's version of Kepler's 3rd Law includes information about the masses of the objects involved.
P2 = 4 But, in the case where one object is much less massive than the other (m2 << m1) this simplifies to
2/G(m1 + m2) * a3 P2 = 4 In the case of the planet Bajor and the star it orbits we'll assume this is the case.2/Gm1 * a3 So again, doing the problem with ratios will save much time and hassle. For the Earth around our Sun the equation reads:
P 2 = 42/GM
* a3
For the planet Bajor the equation reads
PB2 = 4 2/GM* * aB3
So the ratio between the two equations reads
(PB/P )2 = M/M* * (aB/a)3
Now, M* = 15M
, so we plug in the values we know...
(268 days/365.26 days)2 = M /15M * (aB/1 AU)3
Now solve for aB...
aB = {15*(268/365.26)2}1/3 * 1 AU = 2.00 AU
How much does it weigh on Mercury?
(11 points)Mercury's mass is 0.0553 times that of Earth, and Mercury's radius is 0.3824 times Earth's radius. If a goat weighs 120 lbs on Earth, how much does it weigh on Mercury? (HINT: How strong is the gravitational force on the object when on Mercury's surface compared with when on Earth's surface? Use ratios!)
Weight is the force that gravity exerts on an object. Newton's Universal equation for gravity states that
, m2 as the mass of the object (in this case a goat), mg, and the distance between them is the radius of the planet, R. Thus on Earth the goats weight is given by
= - GMmg/R2
Likewise, on Mercury the goats weight would be
= - GMmg/R2
Where, , is the symbol for Mercury. So, let's make a ratio again. Hmm, seems like these ratio things are pretty darned useful...
/F = - GMmg/- GMmg * R2/R2
= 0.0553M, and R = 0.3824R. Plugging those in and simplifying the equation gives...
= (0.0553M/M) *(R/0.3824R)2* F
= 120 lbs
= (0.0553)*(1/0.3824)2* 120 lbs = 45.4 lbs
Laser show
(13 points)The laser pointer used in class emits red light having a wavelength of 6500 Å. (NOTE: 1 Å = 10-10 m)
- What is the frequency of this radiation?
Recall that the relationship between frequency and wavelength of a wave depends on its speed. For light we write
= c - If a green laser (5000 Å) is used in another class, is the frequency lower, higher, or the same as that of the red laser?
By the same method as part (a) you will find that for the green laser
- Through a vacuum, does green light travel faster, slower, or at the same speed as the red light?
All light travels at exactly the same speed through a vacuum. This includes red, green, infrared, radio, X-rays, etc. (i.e. all of the electromagnetic radiation).
The energetic electron
(15 points)Consider a hypothetical atom with an electron whose possible energy levels are shown below. The energy (in arbitrary units) of each higher level is given relative to the ground (lowest state).
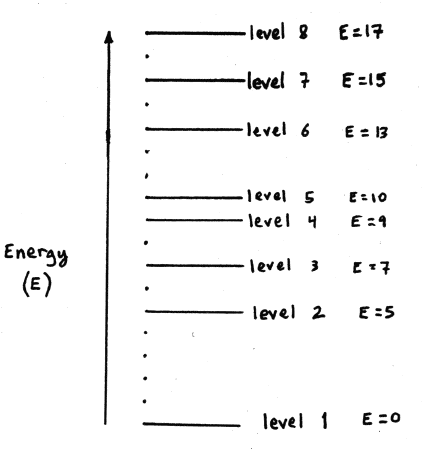
- When the electron jumps from level 1 to 3 it must absorb a photon having a specific energy. Identify another electronic transition that requires the absorption of a photon with the same energy.
Level 1 has is an energy E1 = 0 and level 3 has an energy E3 = 7. So the difference between the two levels is the energy a photon must have to be absorbed and move an electron from level 1 to level 3. That difference we write as
E1-3 = 7. ( is the mathematical symbol used to indicate the amount of change in a quantity). So this is just a matter of finding the differences for all transitions in these 8 levels. When you do that you discover that there is only one other transition with the same energy difference, and that is E5-8 = 7
- Suppose the electron jumps from level 8 to 4, followed by level 4 to 3. What is the ratio of the energies of the photons emitted.
Moving from level 8 to level 4 gives off a photon with energy
E8-4 = 17 - 9 = 8, and Moving from level 4 to level 3 gives off a photon with energy E4-3 = 9 - 7 = 2. So the ratio is
E8-4/E4-3 = 8/2 = 4 - If the electron subsequently jumps from level 3 to 2, can the emitted photon be absorbed by another identical atom whose electron is in level 5? Explain carefully.
Moving from level 3 to level 2 gives off a photon with energy
E3-2 = 7 - 5 = 2. If an identical atom nearby had an electron in level 5 its energy would be E5 = 10. If it were to absorb that photon it would have energy E = 12. There are no levels with energy equal to 12. So, No the emitted photon could not be absorbed by an identical atom with an electron in level 5.
- Suppose the wavelength of the photon absorbed when the electron jumps from level 2 to 4 is 10,000 Å. What would be the wavelength of the photon it would have to absorb if it were to jump from level 2 to 6?
The absorbed photon for the transition from 2 to 4 has an energy
E2-4 = 9 - 5 = 4. And it has a wavelength, = 10,000 Å (1 x 10-6 m). The energy that a photon would need to boost the electron up to level 6 from level 2 would be E2-6 = 13 - 5 = 8. Now, wavelength and energy of a photon are related by
E = hc/ So, if we want to know what the wavelength of the photon needed to get to level 6 would be we just need to take a ratio of the energies. E2-4/E2-6 = 4/8 = (hc/ 2-4)/(hc/2-6) = 2-6/2-4 = 2-6/10,000 Å2-6 = 10,000 Å*(4/8) = 5,000 Å
Cool Threads, Man
(11 points)Is a person wearing a blue shirt hotter than one wearing a red shirt? How is this consistent with Wien's Law? If they were characters on Star Trek which would be the first to die?
No, a person wearing a blue shirt is not hotter than a person wearing a red shirt. The light you see that tells your eyes what color a shirt is is not emitted light, but reflected light. Wien's Law is a relation between the temperature and color (wavelength) of emitted light for a blackbody. When you see a shirt to be blue or red it is so because of the chemical dyes in the material that absorb and reflect different colors. Reflected light does not generally give you any information on the temperature of an object.
The last part was just a joke. You didn't have to answer it. On the old Star Trek series whenever there was a landing party it would contain Captain Kirk (gold shirt), Mr. Spock (blue shirt), Dr. McCoy (blue shirt), and Ensign Joe Schmoe (red shirt). The guy in the red shirt was always the first to die.
Telescopes
(15 points)You are an avid amateur astronomer using a reflecting telescope whose collecting mirror is 16 cm in diameter. Let's say that on a clear night you can just barely see star Lisa with this telescope. Star Bart is only 0.01 times as bright as star Lisa.
- What would the diameter of your telescope's mirror need to be in order for you to barely see star Bart?
Star Bart is 100 times dimmer than the 16 cm telescope can see. In order to just be able to see this star we need to collect 100 times more photons. In order to collect 100 times more photons you need 100 times the collecting area. The area of a telescope is related to the diameter: A =
(D/2)2. So let's make a ratio to find out how large our new telescope needs to be.
A?/A16 = 100 = ( And So,(D?/2)2)/((D16/2)2) = (D?/D16)2
D? = 10*D16 = 10*16 cm = 160 cm - Suppose you cannot afford to buy such a large telescope. Could you detect star Bart with photographic film instead of your eye at the focal plane of your small telescope? Explain how.
Yes. Photographic film can collect more photons by waiting for them. Your eye can only add up the light for a short (and fixed) period of time (about 1/30th of a second), but film can be exposed (add up the light) for many hours.
If we assume that the film is as sensitive as your eyes then you would need to wait 100 times longer than your eyes can see, about 3 seconds.
- Explain why a CCD (charge-coupled device) would allow you to detect even fainter stars using your small telescope, using the same exposure time as with the photographic film.
The CCD can detect fainter stars because it is much more efficient. Only a few percent of the photons incident on film cause the film to react, whereas 80 to 90 percent are detected on a CCD.
Since the efficiency factor for a CCD is nearly 100 times that of an eye or film, we would only have to expose the CCD for about 1/30th of a second to see star Bart. This is the same frame rate as video (no accident, since speed of video is tailored to the speed of the eye). So, we should be able to see star Bart by putting a CCD video camera at the focus of the 16 cm telescope.
- Now consider the Hubble Space Telescope. What were 3 reasons for wanting to have such a telescope in space?
Earth's atmosphere blocks many wavelengths of light detectable by such a telescopes (ultraviolet and near-infrared). Getting above the atmosphere is necessary to see those wavelengths.
Earth's atmosphere also causes incoming light to scatter about or blur. This limits a telescope's spatial resolution no matter how big the primary mirror. In space, better spatial resolution can be achieved with only moderate sized telescopes. HST does about 10 times better than ground based telescopes.
Earth's atmosphere absorbs some light, making faint objects more difficult to detect. The atmosphere also glows from scattered moonlight, city lights, aurorae, sunlight, and molecules in the air that emit at various wavelengths (especially infrared). This makes it even more difficult to see faint objects. In space, a telescope can see much fainter and hence farther into the Universe's past.
Sunspots
(12 points)A sunspot may be 2000 K cooler than the surrounding photosphere of the Sun (whose temperature is about 6000 K).
- How much energy does the sunspot emit per second, per unit area, relative to the surrounding photosphere?
Sounds like a ratio is called for. In class we discussed this very thing. We saw that there is a relationship between the temperature of a black body emitter and the amount of energy per unit area per unit time,
, it emits. It's called the Stefan-Boltzmann Law:
= 
T4So if the photosphere's temperature is 6000 K and the sunspot's is 2000 K less, then the sunspot's temperature is 4000 K. So let's take the ratio of energy output for each region:
ss/ph = (Tss4)/(Tph4) = (Tss/Tph)4 = (4000 K/6000 K)4 = (2/3)4 = 0.1975
ss = 0.2*ph
So, the sunspot only puts out 20% the amount of radiation as the surrounding photosphere.
- Thus, is the sunspot totally black? Why does it look dark?
Nothing at a temperature of 4000 K is black. The sunspots do indeed put out a large amount of energy. It looks dark next to the photosphere as a pure consequence of contrast. The photosphere puts out 80% more light per unit surface area per unit time than the sunspot and so appears so much brighter that it makes the spot look dark in comparison.
'Tis The Season
(10 points)What would the seasons be like if the Earth's axis of rotation were perpendicular to Earth's orbital plane? Would they be more or less extreme than they are now? Explain.
The seasons would be less extreme, in fact there would be no seasons at all! The entire reason that seasons occur is because any given place on Earth receives different amounts of energy from the Sun throughout the year. This occurs because Earth's axis is tilted 23.5° from perpendicular. When the axis is perpendicular any given place on Earth will receive the same amount of energy all year long. The Sun would rise and set everyday at 6 o'clock, giving 12 hours of light and dark. The Sun would also always rise from due East and set due West, there would be no change in this position throughout the year. Thus there would be no large changes in the climate. Earth's change in distance from the Sun during the year would have such a slight effect that it would not influence the climate noticeably.