

Up: No Title
Previous: The Mass of the
In class we learned that for a critical Universe (i.e. one with exactly E = 0)

where R(t) is a scale factor indicative of the size of the Universe at time t.
-
How does
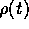 scale with R(t)? If the current density, i.e.
scale with R(t)? If the current density, i.e.  (today), is denoted
(today), is denoted 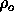 , and the current scale factor is denoted
, and the current scale factor is denoted 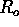 , write
, write 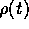 as a function of
as a function of 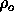 ,
, 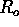 , and R(t).
, and R(t).
-
Plug this result into (1). Rearrange the equation into the form
(function of R)dR = (function of t)dt
and integrate to get R(t).
-
Use Hubble's law and the result of part 2 to find the age of the Universe,
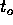 , in terms of
, in terms of 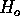 . Let
. Let 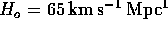 . Express
. Express 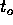 in years.
in years.
Now (1) is valid only for a critical E = 0 Universe. A more general calculation, allowing for nonzero energy, would show

where
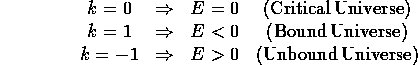
-
Now consider a universe with no matter. Evaluate (2) to find R(t).
-
What is the age of the Universe,
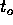 , as a function of
, as a function of 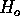 for this empty model? What is
for this empty model? What is 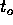 in years if
in years if 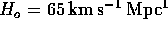 ?
?
-
Given that the real Universe does contain goats and other matter, what can you say about the real age of the Universe relative to what you found in part 5?
We can make (2) even more general by including a term with Einstein's cosmological constant:
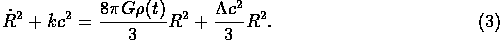
-
Plug your answer for part 1 into (3). take the derivative with respect to time of both sides of the equation to show

-
Use the defininitions of the acceleration parameter
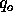 , the matter density parameter
, the matter density parameter 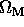 , and the vacuum energy density parameter
, and the vacuum energy density parameter 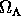 from your notes (you know, the ones that you took in class) with equation (4) to find
from your notes (you know, the ones that you took in class) with equation (4) to find 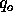 as a function of
as a function of 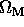 and
and 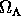 .
.
There is considerable observational evidence and theoretical research pointing toward the notion that we live in a critical k = 0 Universe.
-
If this is true, what is
 ? Express
? Express 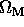 in terms of
in terms of 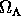 .
.
-
Let's say that some intrepid astronomer measures
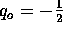 . What are the values of
. What are the values of 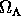 and
and 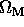 ? What are the implications to the expansion and fate of the Universe?
? What are the implications to the expansion and fate of the Universe?


Up: No Title
Previous: The Mass of the
Astronomy 7
Thu Nov 11 17:12:29 PST 1999
![]()
![]()
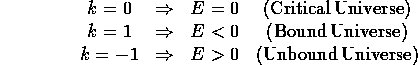
![]()
![]()