next up previous
Next: Velocity of Barnard's Star Up: No Title Previous: Core Collapse by Evaporation

Measuring the Galactic Rotation Curve


Figure: 3

Fig. 3 shows the distribution of neutral hydrogen maxima (shaded curves) in the spiral arms of our Galaxy. The position of the Sun is marked by the symbol tex2html_wrap_inline267 and its circular orbit is plotted as a dashed curve.

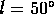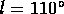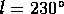  1. Draw the 21-cm line profiles (i.e. 21-cm intensity as a function of frequency tex2html_wrap_inline269 ) you would expect to observe in the directions tex2html_wrap_inline271 , tex2html_wrap_inline273 , and tex2html_wrap_inline275 . Label the points on these profiles corresponding to spiral arms. Do not undertake any detailed velocity calculations, but make sure that the profiles are qualitatively accurate and display all the necessary features in correct positions.
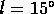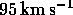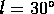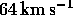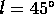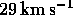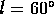The following maximum velocities (relative to the Local Standard of Rest) of neutral hydrogen gas are observed by measuring 21-cm emission along certain lines-of-sight: (i) tex2html_wrap_inline277 , tex2html_wrap_inline279 ; (ii) tex2html_wrap_inline281 , tex2html_wrap_inline283 ; (iii) tex2html_wrap_inline285 , tex2html_wrap_inline287 ; (iv) tex2html_wrap_inline289 , tex2html_wrap_inline291 ; (iv) 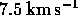tex2html_wrap_inline293 , 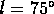tex2html_wrap_inline295 .
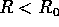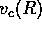  1. Compute and then plot the rotation curve of the Galaxy interior to the Sun ( tex2html_wrap_inline297 ) using these data. Remember, the rotation curve is a graph of circular speed tex2html_wrap_inline299 as a function of Galactic radius R.
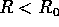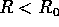  2. Assuming that the mass distribution is spherically symmetric for tex2html_wrap_inline297 , compute and then plot a graph of the mass M(R) enclosed within a radius R, as a function of tex2html_wrap_inline297 .
  3. Evaluate numerically the total mass interior to the Sun. Express your answer in solar masses.
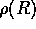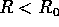  4. Compute and then plot a rough curve of mass density tex2html_wrap_inline311 as a function of tex2html_wrap_inline297 .

Astronomy 7
Tue Oct 19 13:15:33 PDT 1999