


Next: Measuring the Galactic Rotation
Up: No Title
Previous: Binary Formation in Globular
Evaporation of stars from a globular cluster causes the
cluster to shrink over time.
-
Write a paragraph explaining how this happens physically.
Start from first principles and include every step
in your reasoning. At the same time, be concise
(
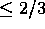 page including any diagrams);
aim for clarity through economy of expression.
(This exercise is intended to help you practise
writing `essay paragraphs' in exams.)
page including any diagrams);
aim for clarity through economy of expression.
(This exercise is intended to help you practise
writing `essay paragraphs' in exams.)
-
Suppose evaporation occurs sufficiently slowly for the cluster
to remain in equilibrium at every stage of the collapse.
Using the virial theorem, express the total mechanical energy
of the cluster, E(t), in terms of its mass M(t)
and radius R(t). Your answer will be approximate;
ignore factors of order unity.
-
Each evaporating star carries away very little total mechanical
energy as it escapes the cluster. Explain why,
physically, this is so.
-
Use 2. and 3. to show that the rate of change of the
cluster radius is related to the mass loss rate by
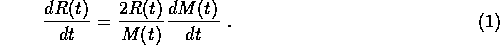
-
Also use 2. and 3. to relate M(t) and R(t)
to the initial mass
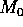 and radius
and radius 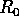 by
by

The mass loss rate is given approximately by

where 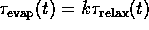 ,
with
,
with 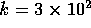 ,
is the evaporation time.
The relaxation time
,
is the evaporation time.
The relaxation time  is
given by the Spitzer-Hart formula (see lecture notes)
is
given by the Spitzer-Hart formula (see lecture notes)
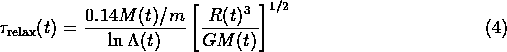
with 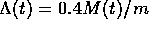 , provided that
all stars in the cluster have the same mass m.
, provided that
all stars in the cluster have the same mass m.
-
Why does
 change with time t
as the cluster evolves?
Why is k roughly constant?
Please give physical, not mathematical, explanations.
Be precise.
change with time t
as the cluster evolves?
Why is k roughly constant?
Please give physical, not mathematical, explanations.
Be precise.
-
Combine (1)-(4) to eliminate M(t) and obtain a
first-order differential equation for how R(t)
evolves with time.
-
Assume
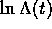 is constant with time;
logarithms change very slowly.
Integrate the equation in 7. and show that R(t)
is of the form
is constant with time;
logarithms change very slowly.
Integrate the equation in 7. and show that R(t)
is of the form

Express 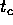 in terms of G, m,
in terms of G, m, 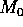 , and
, and 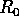 .
Sketch R(t) as a function of t.
.
Sketch R(t) as a function of t.
-
Evaluate numerically how long it takes for a typical
globular cluster to collapse to a point.
Then repeat your estimate for just the core of a cluster.
Use typical numbers such as those in the lecture notes.
Comment.
-
Apply the virial theorem to obtain V(t), the characteristic
stellar speed, in terms of R(t) and hence G,
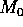 ,
,
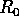 and
and 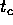 .
Sketch V(t) as a function of t.
What is the value of
.
Sketch V(t) as a function of t.
What is the value of 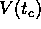 ? Is this realistic?
? Is this realistic?
In reality, a globular cluster does not collapse to a point.
Its end state is a single close binary with, say,
 and
and
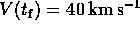 ,
as indicated by numerical simulations.
,
as indicated by numerical simulations.
-
Using 8., 10., and
 ,
evaluate
,
evaluate 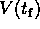 numerically.
You should get a much larger speed than
numerically.
You should get a much larger speed than
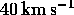 .
Can you suggest two reasons why the simple theory
of this problem does not predict the end state of
core collapse correctly?
.
Can you suggest two reasons why the simple theory
of this problem does not predict the end state of
core collapse correctly?



Next: Measuring the Galactic Rotation
Up: No Title
Previous: Binary Formation in Globular
Astronomy 7
Tue Oct 19 13:15:33 PDT 1999
![]()
![]()
![]()
![]()
![]()
![]() ,
with
,
with ![]() ,
is the evaporation time.
The relaxation time
,
is the evaporation time.
The relaxation time ![]() is
given by the Spitzer-Hart formula (see lecture notes)
is
given by the Spitzer-Hart formula (see lecture notes)
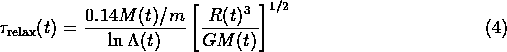
![]() , provided that
all stars in the cluster have the same mass m.
, provided that
all stars in the cluster have the same mass m.
![]()
![]() in terms of G, m,
in terms of G, m, ![]() , and
, and ![]() .
Sketch R(t) as a function of t.
.
Sketch R(t) as a function of t.