


Next: Copernicus versus Ptolemy
Up: No Title
Previous: Launching Satellites
Consider a body, of mass m, attached to one end of a spring
with spring constant 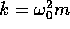 .
The other end of the spring is fixed and the body is set
into motion about the fixed point with angular
momentum per unit mass J and total mechanical energy
per unit mass E.
.
The other end of the spring is fixed and the body is set
into motion about the fixed point with angular
momentum per unit mass J and total mechanical energy
per unit mass E.
-
Using as a guide the planetary Kepler problem from lectures,
show that the body describes an orbit given by
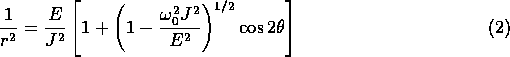
in the 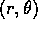 plane.
plane.
-
What shape is this locus? Draw a labelled diagram in the
(x,y) plane.
-
What condition must be satisfied by
 , J, and E
in order for the orbit to be bound?
, J, and E
in order for the orbit to be bound?
-
Again using lectures as a guide, derive an effective
potential per unit mass,
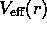 , for the body
satisfying
, for the body
satisfying

Interpret your answer to the previous question in terms of
this effective potential.
Now imagine a planetary system in which the force of gravity
is spring-like, i.e. it is attractive and directly
(not inversely!) proportional to the square of
the separation between two
bodies. (Needless to say, this is not a real planetary system,
but it is very important in other contexts, as you will see
later in the course.)
-
Derive the equivalent of Kepler's Third Law for this
planetary system. What is special about your result?
-
What would be the motion of Mars in the sky as seen from Earth
if the Earth and Mars were in this planetary system?
Bryan J. Mendez
Fri Aug 27 17:24:54 PDT 1999
![]() .
The other end of the spring is fixed and the body is set
into motion about the fixed point with angular
momentum per unit mass J and total mechanical energy
per unit mass E.
.
The other end of the spring is fixed and the body is set
into motion about the fixed point with angular
momentum per unit mass J and total mechanical energy
per unit mass E.
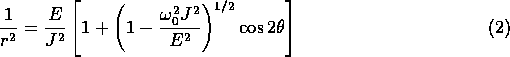
![]() plane.
plane.
![]()