Precision CCD Astrometry

Precision CCD Astrometry

Bryan J. Méndez
and
Patrick Seitzer

Department of Astronomy
The University of Michigan
830 Dennison Bldg.
510 Church St.
Ann Arbor, MI 48109
bmendez@astro.lsa.umich.edu

Abstract

We investigate how accurately absolute stellar proper motions with respect to background field galaxies can be determined using CCD data. R band CCD images of an Abell cluster of galaxies from the MDM 2.4-m are analyzed to determine the random errors in a galaxy's position. We apply the technique to the halo globular cluster Palomar 15, using first epoch data from 1984 and 1985 from CTIO and KPNO, and second epoch data from 1995 from the MDM 2.4-m. We also invesitage the technique's potential for measuring internal stellar motions within other halo globular clusters, NGC 6541 and Omega Centaurus, using first epoch HST data from 1994 and 1995.

Keywords: astrometry...clusters: individual (Abell 427)...globular clusters: individual (Palomar 15, Omega Centaurus, NGC 6541)...instrumentation: detectors...methods: data analysis...methods: observational

Introduction

CCD stellar astrometry has demonstrated 1 millarcsecond positional accuracy (Monet et al. 1992). This level of precision means that proper motions of distant objects can be determined on time scales of 10 years or less. Of primary concern to us is the ability to do such precise astrometry with already existing technology and CCD images. We are interested in using CCD data from the early 1980's as first epoch material to measure proper motions of satellite systems of the Milky Way to study the mass of the Milky Way and the orbital characteristics of the satellites. For example, the cluster Palomar 15 was studied extensively by Seitzer and Carney (1986), and the field shows at least half a dozen background galaxies. With early epoch CTIO and KPNO 4 meter CCD data from 1984 - 1986, we have attempted to measure its absolute proper motion.

This initial work motivated us to study in more detail how accurately stellar positions could be measured with respect to background galaxies. In an ideal world, one would like to have a selection of background point sources like quasars as reference points. However, given the small size of first generation CCD's the probability of having even one quasar in the field of view is extremely small. Thus, to use existing first epoch CCD material, one must use the random distribution of galaxies that occurs in the CCD's field of view. Hence, we observed the galaxy cluster Abell 427 with the MDM 2.4 meter telescope and a thinned, backside illuminated Tektronix CCD in September 1995.

Additionally, Our work has demonstrated that with HST data it is possible to measure internal proper motions within globular clusters as well. We have studied HST frames taken in 1994 and 1995 of globular clusters NGC 6541 and NGC 5139, (Omega Cen), respectively. Indications are that, with 1-2 milliarcsecond measuring accuracy, proper motions should be detectable within 4-5 years of the first epoch.

Palomar 15

The small and faint globular cluster Palomar 15 was studied extensively in the 1980's by Seitzer and Carney (Seitzer and Carney, 1990). Through redshifts and photometry of standard stars in the cluster the its distance and radial velocity were determined. The cluster is at a distance of 37 +/- 5 Kpc with respect to the Sun, and 30 +/- 5 Kpc with respect to the Galactic Center. It has a radial velocity of + 73 km/s. With a proper motion for the cluster we would have the 4 parameters necessary for its absolute space motion. Thus its orbital characteristics could be determined and provide a useful measure of the Galactic mass within. This has been done with larger and closer globular clusters but not for the outer-halo clusters. None have been attempted with CCD data over short temporal baselines.

First Epoch Data

The images of Palomar 15 accumulated by Seitzer and Carney over 1984-1986 were obtained with CCD's on telescopes at KPNO and CTIO. The data were all in B and V band. In 1995, the original reel-to-reel data tapes were successfully read.

Second Epoch Data

In May of 1995, second epoch data of Palomar 15 was obtained on the MDM 2.4 meter telescope and a thinned back-side illuminated CCD (Figure 1). The frames were taken in R band to minimize atmospheric effects.

Fig 1. -- An Average of 10 300sec R-Band exposures obtained with the MDM 2.4 meter telescope and a thinned CCD in May of 1995. At least half-a-dozen background galaxies are visible here and in the first epoch data obtained in 1984 through 1986.

Before proper motions could be computed it was necessary to determine to what precision stellar positions could be measured. Using facilities in IRAF we developed a method for analyzing CCD frames for positional errors. The first step was to decide what centering algorithm to use. We examined positional errors returned by the photometry task phot in the package daphot against their magnitudes. This was done over a grid of centering algorithms and centering box widths. The two algorithms used were gaussian and centroid, and the box widths ranged from 5 - 9. In Figure 2 it can be seen that the larger box widths yield better precision. Centroid gives higher precision for brighter stars but in the range where most stars in the fields lie gaussian is actually better. However, we are uncertain as to how the errors are computed by IRAF, thus we employed another test.

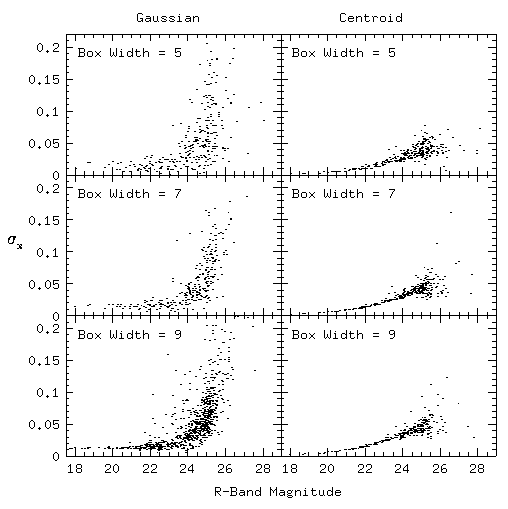
Fig 2. -- Examining the positional errors computed by IRAF against magnitudes showed little preference for centering algorithms. In the end Gaussian centering with a box width of 9 yielded the best results.

From a private conversation with Monet it was determined that the most reliable method of determining the positional errors was to examine the mean error in pairwise differences between stars. The mean error in the mean of individual positions is then

where N here is the number of frames used.

This was done over the grid of centering algorithms for 10 frames of Palomar 15 for the brightest 500 objects in the frames. Histograms were made of the errors to see where the peak in the error would be. This is, of course, strongly dependent on the histogram resolution. It was useful to use a bin width of 615 milliarcseconds to further examine the precision of the various centering options. Figure 3 shows that the peak in errors for gaussian 5 and 7 were very high and thus not useful. Still the guassian algorithm with a box width of 9 actually shows the strongest peak in the first bin. This test was applied at various levels to all of the data discussed in this paper and universally the gaussian centering with a box width of 9 gave the most precise results.

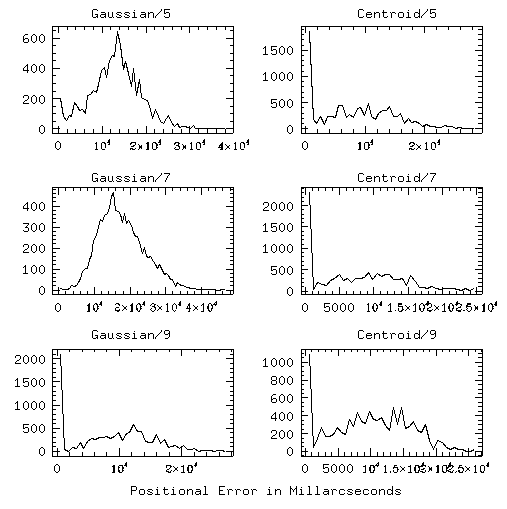
Fig 3. -- Histograms of the mean errors in x and y measurements of the 500 brightest stars in 10 frames of Palomar 15 taken in May 1995 with the MDM 2.4 meter telescope and a thinnned back-side illuminated CCD. These histograms show the difference between the various centering algorithms. The bin width is 615 milliarcseconds. Here it becomes more clear why Gaussian with box width 9 is preferred.

Using the gaussian/9 we then made higher resolution histograms to find the mode in the errors (Figure 4). The bin width used was 0.4 millarcseconds. The errors peak at 1.31 milliarcseconds along CCD rows and 1.25 milliarcseconds along CCD columns. Thus we confirm the previous work by Monet that 1 milliarcsecond precision is possible with existing CCD technology.

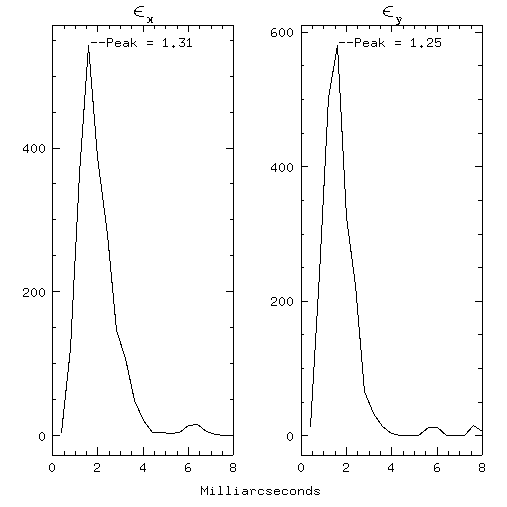
Fig 4. -- Histograms of the mean errors in x and y measurements of the 500 brightest stars in 10 frames of Palomar 15 taken in May 1995 with the MDM 2.4 meter telescope and a thinnned back-side illuminated CCD. The Gaussian centering algorithm with box width 9 was used and the bin width is 0.4 milliarcseconds.

Proper Motions

The standard proper motion formula is
If we assume a tangential velocity of 200 km/s, which is often observed in local halo objects, for Palomar 15 we would then observe a proper motion of 1.14 milliarcseconds per year. So over the a 10 year baseline we should observe a shift in stellar positions with respect to background galaxies of about 10 milliarcseconds. Given the accuracy demonstrated this should be possible.

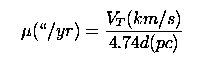
The best frame from 1985 and from 1995 were used to compute a common reference frame. Using utilities in IRAF, reference stars and galaxies were found and matched in order to transform the 1985 data into the reference frame of the 1995 data. Preliminary proper motions were computed but found to be on the order of the errors. A proper motion of 1.4 milliarcseconds was computed using the brightest galaxy in the field as the reference. This is a tangential velocity of 245.5 km/s. However, the error in that galaxy's position was computed at 8 milliarcseconds, corresponding to an uncertainty of 101.3 km/s. So The problem seemed to not originate from the measurement of stellar positions but from the galaxies. Rotations, core radius, and ellipticity are all obviously factors in precise astrometry of galaxies.

Galaxies

From the limited results of the proper motion study of Palomar 15 we saw that this technique showed considerable promise. However, we needed to investigate how well stellar positions could be measured with respect to randomly oriented galaxies. To study this several frames of of the galaxy cluster Abell 427 were obtained again at the 2.4 meter MDM telescope with the same CCD as for Palomar 15. These frames were taken in September 1995. (Figure 5.)

Fig 5. -- Abell 427: An average of 8 300s R-Band exposures also obtained with the MDM 2.4 meter telescope and thinned CCD in September of 1995. Galaxies with a wide range of magnitudes and scale lengths are present, providing an excellent test field for astrometry of galaxies.

Galaxies were separated from stars in the frame using photmetric properties. The task phot in IRAF was run on the frames using two aperture sizes. The differences in magnitudes were then plotted against the magnitude in the inner aperture. As Figure 6 shows the separation was clear; those points lying below a magnitude difference 0.4 are stars and those above are galaxies.

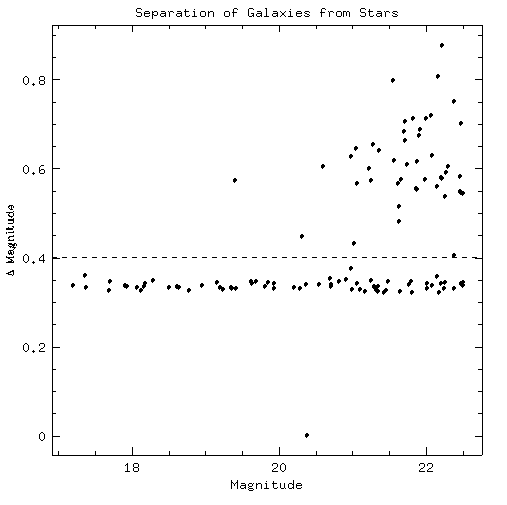
Fig 6. -- Differences of Magnitudes in two different apperatures plotted against the magnitude in one aperature show a clear separation between Galaxies in the cluster Abell 427 and the foreground stars. The dividing line was drawn at a Magnitude difference of 0.4.

Once stars and galaxies were separated from one another analysis of positional errors was conducted as before. The anaylsis was done for pairwise differences of stars with respect to other stars. This showed similar results as before with the mode of the mean error in the mean of measurements of individual stars being around 1 milliarcsecond (Figure 7). Positional errors along CCD rows are 1.70 milliarcseconds and 1.04 along CCD columns. The analysis was also done for pairwise differences of galaxies with respect to stars. Positional errors here were 3-4 times those of stars alone (Figure 8). Positional errors are 3.85 milliarcseconds along both CCD rows and columns.

Fig 7. -- Histograms of the mean errors in x and y measurements of foreground stars in 8 frames of Abell 427 taken in October 1995 with the MDM 2.4 meter telescope and a thinned back-side illuminated CCD.

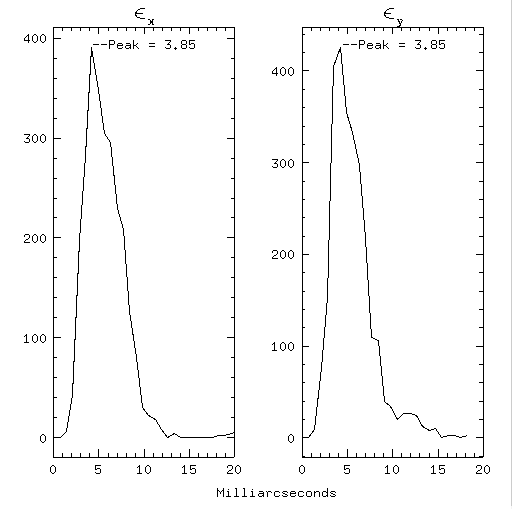
Fig 8. -- Histograms of the mean errors in x and y measurements of foreground stars with respect to galaxies in 8 frames of Abell 427 taken in October 1995 with the MDM 2.4 meter telescope and a thinned back-side illuminated CCD.

Globular Clusters with HST

With millarcsecond precision being demonstrated from ground-based telescopes, without making corrections for atmospheric effects, we suspected that much higher precision could be done from space. We searched through the Hubble Space Telescope archive for frames of globular clusters with the core of the cluster off-center. Our first attempt was with the globular clusters NGC 6541. We used 4 WFPC2 frames taken in October 1994. We focused on the Planetary Camera frames (Figure 9). The Planetary Camera CCD has a resolution of 46 milliarcseconds per pixel. Analysis of the frames showed positional errors of 0.28 milliarcseconds along CCD rows and 0.30 milliarcseconds along CCD columns (Figure 10). This with only 4 frames!

Fig 9. -- An average of 4 Planetary Camera frames of the Globular Cluster NGC 6541 taken in October, 1994 with WFPC2 aboard the Hubble Space Telescope.

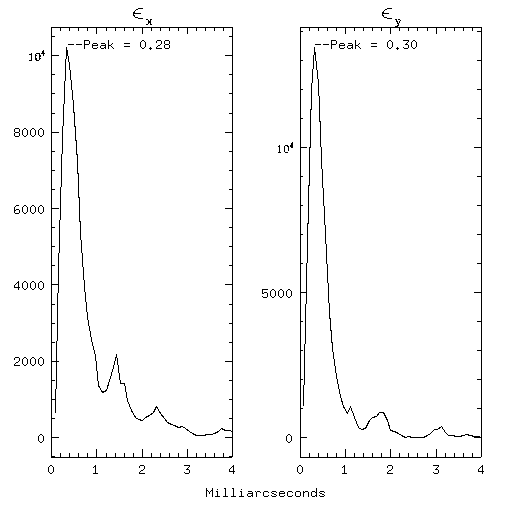
Fig 10. -- Histograms of the mean errors in x and y measurements of the 500 brightest stars in 4 frames of Globular Cluster NGC 6541 taken in October, 1994 with the Planetary Camera CCD aboard the Hubble Space Telescope.

With such high precision possible with HST we realized that not only could proper motions of globular clusters be determined on short temporal baselines but also proper motions of their individual stars. Over a period of 5 or 6 years internal stellar proper motions could be detected. This would greatly increase our knowledge of globular clusters by allowing us to explore their internal kinematics in great detail.

Seitzer is involved in an effort to study the brightest and largest globular cluster orbiting the Galaxy, NGC 5139, Omega Centauri. After having seen the precision possible with HST we looked again through the archives for an image of Omega Centauri. Having found 3 WFPC2 frames from July of 1995 with the rotation such that the core was off center we set about the analysis. We focused on the Wide Field Camera [2] CCD frames (Figure 11). The Wide Field Camera CCD's have a resolution of 100 milliarcseconds per pixel. Analysis of the 3 frames yields positional errors of 0.51 millarcseconds along CCD rows and 0.70 milliarcseconds along CCD columns. With this level of precision possible internal proper motions could be measured in less than 5 years!

Fig 11. -- An average of 3 Wide Field Camera [2] frames of Omega Centauri taken in 1995 with WFPC2 aboard the Hubble Space Telescope.

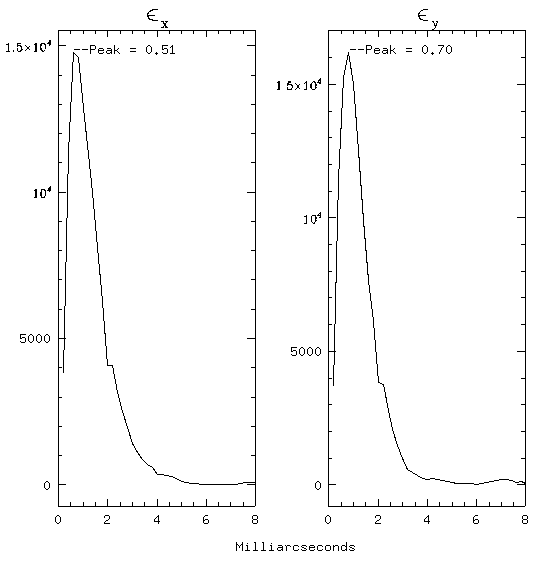
Fig 12. -- Histograms of the mean errors in x and y measurements of the 500 brightest stars in 3 frames of Omega Centauri taken in 1995 with the Wide Field Camera [2] CCD aboard the Hubble Space Telescope.

Future Work

It may yet be possible to measure the proper motion of Palomar 15 with the existing data. Further work could be done to increase the astrometric precision of the background galaxies by accounting for atmospheric refraction. Additionally, more background galaxies may be in the field of view that could be identified by the separation process done for Abell 427. This would increase the statistical significance of a proper motion detection. If a proper motion is determined the cluster's absolute space motion would be known. We would then set about determining its orbit and the mass of the galaxy interior to it.

In another year or two Omega Centauri should have had enough time to show detectable internal proper motions. One orbit on the Hubble Space Telescope would be enough to obtain enough frames to measure stellar positions to the sub-milliarcsecond level. We plan to submit a proposal to obtain second epoch data for Omega Centauri in 1998.

References