Warping of a Disk Galaxy

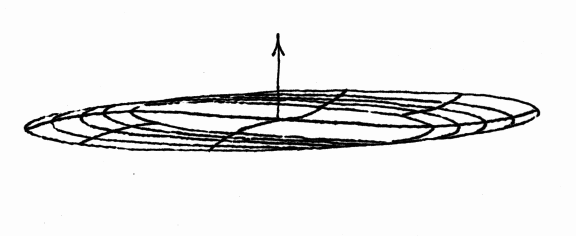
A disk galaxy typically appears flat at visible wavelengths, where the observed light traces the position of stars, particularly young O and B stars. At radio wavelengths, where the observed radiation traces the position of gas (e.g. neutral hydrogen), many galaxies display a warp. Figure 1 illustrates what a warp looks like when viewed edge-on. The disk of the galaxy turns up at one edge and down at the other, just like the brim of a sombrero hat.

Figure: 1

Warped disks are common. For example, all of the spiral galaxies in our Local Group (the Milky Way, Andromeda, and M33) are warped. At the same time, noone really knows what causes a warp to develop. The aim of this problem is to analyse one plausible theory that has been advanced recently.

Suppose we model a disk galaxy as a combination of an infinite disk and an infinite halo of stars. Both the disk and the halo are assumed to be cylindrically symmetric. However, their axes of symmetry are misaligned, as shown in Figure 2 (edge-on view). The disk is symmetric about the z axis, while the symmetry axis z' of the halo is inclined to the z axis by an angle I.

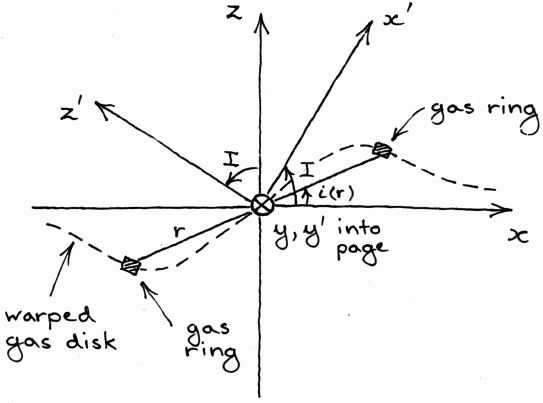
Figure: 2

Now consider a thin ring of gas, of radius r, inclined at an angle i to the x axis as shown in Figure 3.

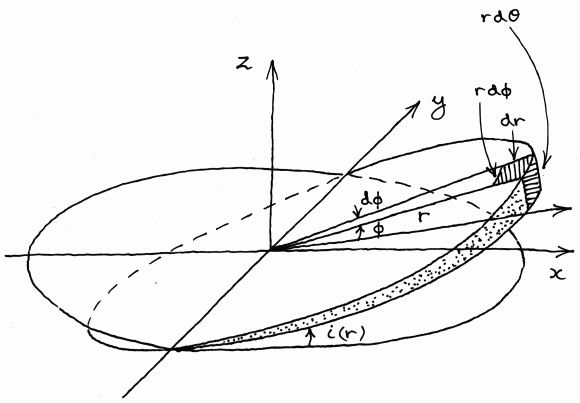
Figure: 3

In general, the nonspherical geometry of the system implies that there is a nonzero net torque acting on the gas ring. Nevertheless, it turns out that, for every value of r, there is a value of i, written as i(r), for which the net torque acting on the gas ring vanishes, because the torque exerted by the halo exactly cancels the torque exerted by the disk. The gas collects at the positions where the torque vanishes, forming a stable configuration. We calculate the shape of the configuration, i(r), in this problem.

1. (Easy.) Using symmetry arguments, sketch roughly the direction of the gravitational fields of the disk and halo at a selection of points in the galaxy. Draw the system edge-on, as in Figure 2. From your sketch, show that the distribution of gas cannot be flat, like the disk, because a flat gas distribution experiences a nonzero net torque.

The first step in the calculation is to calculate the gravitational acceleration due to the halo at an arbitrary point . For this, we need to assume a gravitational potential for the halo that is cylindrically symmetric about the z' axis. One such simple potential is

where and are constants describing the central potential and characteristic radius of the halo respectively, and q is a geometric factor.

2. (Easy.) On a fresh set of (x',y',z') axes, sketch the surfaces of constant . Aim to get the general shape correct; do not try to be quantitative.
3. (Easy.) From Figure 2, show that the coordinates (x',y',z') of any point in the halo `frame' can be related to its coordinates (x,y,z) in the `disk' frame by

   

4. (Extra credit. Not hard, but the algebra is tedious; do not spend too long on it if you feel like you are going nowhere.) First re-express , given by (1), in terms of (x,y,z) coordinates using your results from 3. Then calculate the gravitational acceleration due to the halo using the results , , and . (The gravitational acceleration is the negative gradient of the potential.) Show that

   

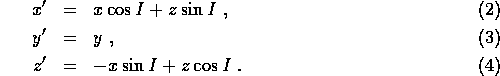
The second step in the calculation is to calculate the gravitational acceleration due to the disk at an arbitrary point . We assume that the disk has infinite diameter, zero thickness, and surface mass density (units: ).

5. (Easy.) By symmetry arguments, what is the direction of above and below the disk? Explain your reasoning.
6. (Easy.) Calculate using Gauss's Law. Please explain all steps in your reasoning carefully. You ought to find

   

   with the plus sign for z<0 and the minus sign for z>0. (Hint: for a Gaussian surface, you may wish to use a cylinder of height 2z and cross-sectional area A bisected horizontally by the disk.)

The third step in the calculation is to calculate the torque per unit mass, , exerted by the disk and halo on a gas ring of radius r and inclination i, shown in Figure 3.

7. (Extra credit.) Divide the ring into infinitesimal elements of angular size as shown in Figure 3. Show that the torque per unit mass exerted on the infinitesimal element at angular position is

   

   where

   

   and is the total gravitational acceleration due to disk and halo.

8. (Extra credit.) Using equations (5), (7) and (8), show that the torque per unit mass on the whole ring due to the halo has zero x and z components and a y component given by

   

9. (Easy. Be careful with the algebra, though.) Using equations (6), (7) and (8), show that the total torque per unit mass on the whole ring due to the disk has zero x and z components and a y component given by

   

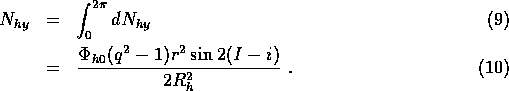
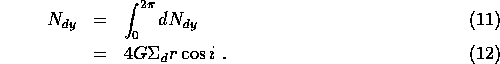
We are finally in a position to calculate the shape of the warp of the galactic gas. Recall that the shape of the warp is described by the variation of the inclination angle i(r) as a function of radius r.

10. (Easy.) Given the total torque exerted by the disk [eq. (12)] and the halo [eq. (10)], show that the following condition holds for a stable gas ring at radius r:

    

11. (Easy.) Graph i(r) as a function of for the special case , . You ought to see a nice warp! [Hint: it is hard to solve for i(r) as a function of r. So do the opposite: solve for r(i) as a function of i. Take a set of i values in the range , calculate r for each value, plot r as a function of i, and then turn the graph on its side to get i as a function of r.]

(I tried to break up the above question into manageable pieces and provide partial results, so that you can readily leave out any part on which you get stuck and still do the other parts. Annoyingly, calculations involving disk galaxies tend to become messy because of the absence of spherical symmetry! Please be sure to try the parts labelled `easy', but don't be disappointed if some of the other parts cause you trouble.)