

Next: Eclipsing Binaries
Up: No Title
The double-neutron-star binary discussed in lectures
contains a neutron star from which
we detect a pulsed radio signal,
named PSR B1913+16,
and a second neutron star which we cannot see.
The radio pulses arise because PSR B1913+16 emits a
beam of radio waves along its magnetic axis,
which is tilted with respect to its rotation axis,
and the beam sweeps past the Earth once per
neutron-star rotation, as in Fig. 2.1.
(Just like a lighthouse.)
The second neutron star probably emits a beam of radio
waves too, but this second beam presumably never sweeps
past the Earth.
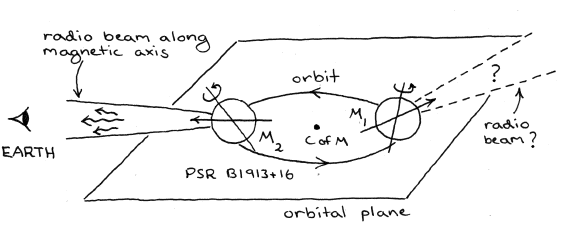
Figure: 2.1
PSR B1913+16 rotates once every
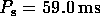 as measured by an observer in its
orbital rest frame.
However, the separation of the radio pulses measured at Earth
(i.e. the pulse period)
fluctuates between
as measured by an observer in its
orbital rest frame.
However, the separation of the radio pulses measured at Earth
(i.e. the pulse period)
fluctuates between 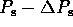 and
and 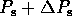 , as shown in Fig. 2.2,
mainly due to the Doppler effect.
(This is related to, but not the same as, the Doppler shift
of spectral lines discussed in lectures.)
, as shown in Fig. 2.2,
mainly due to the Doppler effect.
(This is related to, but not the same as, the Doppler shift
of spectral lines discussed in lectures.)
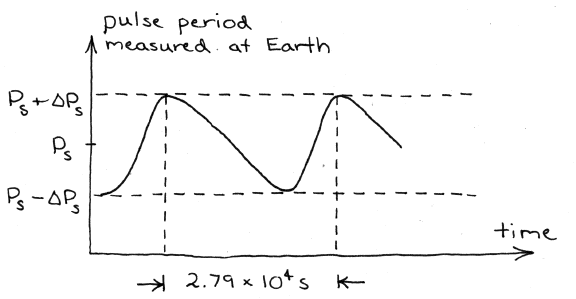
Figure: 2.2
-
Redraw Fig. 2.2 and mark three points where PSR B1913+16
is moving
(i) towards Earth with maximum velocity along
the line of sight,
(ii) away from Earth with maximum velocity along
the line of sight,
and (iii) transverse to the line of sight.
-
What property of the binary system corresponds to
the time interval of
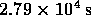 ?
?
By studying the detailed shape of the curve in Fig. 2.2,
including general relativistic effects,
it is possible to deduce the eccentricity of the binary orbit,
e=0.617,
and the masses of the two neutron stars,
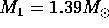 and
and 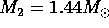 .
(
.
( 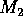 is PSR B1913+16.)
is PSR B1913+16.)
-
Using your answer to part 2. and the data in
the preceding paragraph, calculate the lengths of the
semimajor and semiminor axes of the orbit of
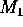 .
Then do the same for
.
Then do the same for 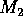 .
.
-
Using your answer to part 3.,
draw approximately to scale the two stellar orbits,
placing the centre of mass at the origin.
Choose your scale wisely so that the two orbits fit on a page
and can be seen without a magnifying glass!
In reality,
the pulse-period fluctuations 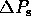 in Fig. 2.2
are known to great precision;
the pulse period is measured to more than ten decimal places
(!) using an atomic clock.
However, the preceding parts of the question contain
enough information for us to calculate
in Fig. 2.2
are known to great precision;
the pulse period is measured to more than ten decimal places
(!) using an atomic clock.
However, the preceding parts of the question contain
enough information for us to calculate
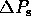 ourselves.
ourselves.
Firstly, we need to calculate the maximum velocity of
PSR B1913+16 along our line of sight.
Assume for simplicity, here and in what follows,
that the orbital plane is inclined edge-on to the line of sight
and the semimajor axis is transverse to the line of sight.
(In reality, this is not the case;
the inclination angle i
is known to be 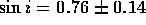 .)
Note that we cannot just apply the results of Shu, Problem 10.1,
because that problem pertains to circular orbits (e=0).
.)
Note that we cannot just apply the results of Shu, Problem 10.1,
because that problem pertains to circular orbits (e=0).
-
It was shown in lectures that the relative position of the
two stars,
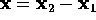 , satisfies the
1-body Kepler equation of motion
, satisfies the
1-body Kepler equation of motion
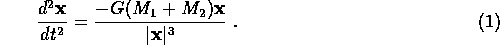
Write down without proof
the energy equation corresponding to (1).
(Adapt eq. 3 on p. 23 of the lecture notes.)
-
By expressing E in terms of the semimajor axis a
(adapt the result from p. 25 of the lecture notes),
show that the energy equation corresponding to (1)
takes the form
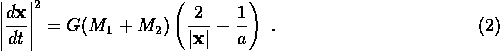
-
Explain in words at what point in the orbit the velocity
along the line of sight is a maximum.
Substitute into (2) the value of
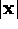 at this point
and show that one has
at this point
and show that one has
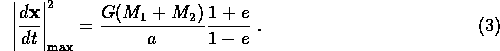
-
The previous result is the maximum velocity of the
relative position vector
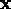 .
Using the results presented in lectures,
relate the actual position
.
Using the results presented in lectures,
relate the actual position 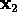 of PSR B1913+16
to the relative position
of PSR B1913+16
to the relative position 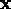 (with the centre of mass at the origin).
Hence find an expression for the maximum value of the
velocity of
(with the centre of mass at the origin).
Hence find an expression for the maximum value of the
velocity of 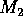 (i.e. PSR B1913+16).
(i.e. PSR B1913+16).
-
Evaluate numerically the maximum value of the
velocity of PSR B1913+16.
Express your answer in
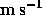 .
.
Now that we know the maximum velocity of PSR B1913+16,
we relate it to the Doppler shift of the pulse period,
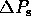 .
.
Consider a flashlight blinking periodically, with period
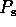 in its rest frame.
Suppose that, at t=0, it blinks on at a distance L
from the Earth, moving towards the Earth with speed V.
in its rest frame.
Suppose that, at t=0, it blinks on at a distance L
from the Earth, moving towards the Earth with speed V.
-
Find an expression, in terms of L and c,
for the time
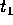 when an observer on Earth sees the
first flash from the flashlight.
Find an expression, in terms of L, V,
when an observer on Earth sees the
first flash from the flashlight.
Find an expression, in terms of L, V, 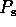 and c,
for the time
and c,
for the time  when an observer on Earth sees the
second flash from the flashlight.
(A quick diagram will help you answer this question.)
when an observer on Earth sees the
second flash from the flashlight.
(A quick diagram will help you answer this question.)
-
Using the results of part 10.,
find an expression (in terms of V,
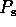 and c)
for the period of the blinking flashlight measured
at Earth.
and c)
for the period of the blinking flashlight measured
at Earth.
-
Using the results of parts 9. and 11.,
evaluate
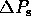 in Fig. 2.2 numerically.
Express your answer in
in Fig. 2.2 numerically.
Express your answer in 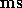 .
.


Next: Eclipsing Binaries
Up: No Title
Astronomy 7
Fri Sep 24 15:39:08 PDT 1999

![]() as measured by an observer in its
orbital rest frame.
However, the separation of the radio pulses measured at Earth
(i.e. the pulse period)
fluctuates between
as measured by an observer in its
orbital rest frame.
However, the separation of the radio pulses measured at Earth
(i.e. the pulse period)
fluctuates between ![]() and
and ![]() , as shown in Fig. 2.2,
mainly due to the Doppler effect.
(This is related to, but not the same as, the Doppler shift
of spectral lines discussed in lectures.)
, as shown in Fig. 2.2,
mainly due to the Doppler effect.
(This is related to, but not the same as, the Doppler shift
of spectral lines discussed in lectures.)
![]() .)
Note that we cannot just apply the results of Shu, Problem 10.1,
because that problem pertains to circular orbits (e=0).
.)
Note that we cannot just apply the results of Shu, Problem 10.1,
because that problem pertains to circular orbits (e=0).
![]()
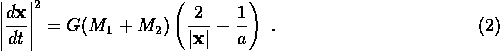
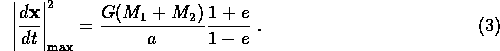
![]() in its rest frame.
Suppose that, at t=0, it blinks on at a distance L
from the Earth, moving towards the Earth with speed V.
in its rest frame.
Suppose that, at t=0, it blinks on at a distance L
from the Earth, moving towards the Earth with speed V.