Child on a Swing

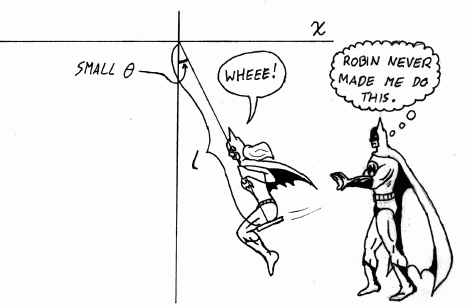
Consider a child of mass m sitting on a swing of length l, as in Figure 2.1. Suppose the child is being pushed and pulled by her brother with a force .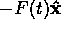

1. What other forces are acting on the child?
2. Write down the x and y components of Newton's equation of motion for the child.
3. For small angles of swing, show that the x position of the child satisfies

   

   where g is the acceleration due to gravity at the Earth's surface.

Suppose that the brother pushes and pulls in a periodic fashion, with 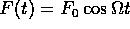. Also suppose that the initial position and velocity of the child are 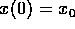and 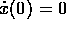. The child's position as a function of time is then given by

(You do not need to prove this. However, if you wish to convince yourself that it is correct, just substitute x(t) into (1) and check that the left-hand side equals the right-hand side, then check that it satisfies the stated initial conditions. An equation like (1) with a second derivative in it must always be accompanied by two initial conditions to specify a solution.)

4. Take and . Draw a sequence of diagrams at times 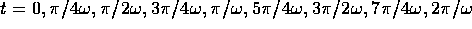showing the successive positions of the swing and the direction and relative magnitude (as an arrow) of F(t) at each position. (Draw the swing positions and arrows roughly to scale, but don't be too fussy.)
5. Redo the above question for 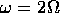and times .
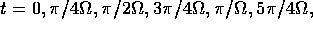
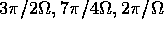6. What happens when 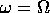? Is this realistic?
7. Describe in your own words, as fully as you can, the analogy between the child on a swing and, say, the 2:1 orbital resonance between some hypothetical asteroid and Jupiter. (There are many equally valid ways of answering this question. Answer it in your own way.)