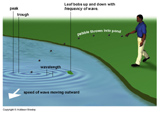
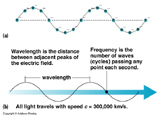
Properties of waves
Wavelenth =
(greek "lambda") = distance from one crest to another. Typical units for are angstroms, 1 Å = 10-10 m = 0.1 nanometers (nm).Monday, June 10th 2002. Reading: Cosmic Perspective Chapters 6 & 7
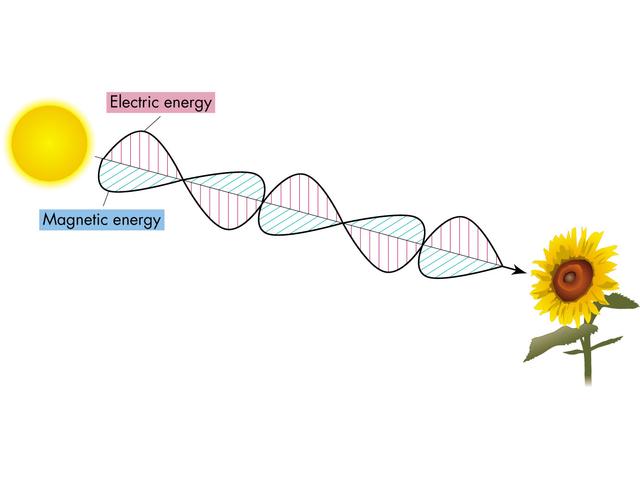
Changing electric fields create magnetic fields, and changing magnetic fields induce changing electric fields. If a charge accelerates the electric field around it will change, creating a magnetic field, which as it forms and collapses with induce an electric field, and an Electromagnetic wave is born...
Properties of waves
Wavelenth = (greek "lambda") = distance from one crest to another. Typical units for are angstroms, 1 Å = 10-10 m = 0.1 nanometers (nm).
Frequency = 
(Greek "nu") = number of crests/troughs passing some fixed point per unit time. Typical unit for frequency is hertz, 1 Hz = 1 s-1. [NOTE: -1 = 1/ = P = Period = length of time between the passing of one crest to another as seen from a fixed point]
Speed: the speed, v, of a wave is the distance that a crest travels per unit time. We can write that in terms of wavelength and frequency as
= v = c
Visible light is the light that human eyes are sensitive to. It comes in colors as seen when white light is passed through a prism and broken into a rainbow.
Different colors correspond to electromagnetic waves having different wavelengths ().
Wavelengths of the visible colors:
| Color | (Å) |
| Red | 7000 |
| Yellow | 5800 |
| Green | 5000 |
| Blue | 4800 |
| Violet | 4000 |
| Name | (meters) |
| Gamma-rays | < 10-11 |
| X-rays | 10-11 - 10-8 |
| Ultraviolet (UV) | 10-8 - 4 x 10-7 |
| Visible (Optical) | 4 x 10-7 - 7 x 10-7 |
| Infrared (IR) | 7 x 10-7 - 10-3 |
| Microwave | 10-3 - 10-2 |
| Radio | 10-2 - 104 + |
Collectively, lots of photons having the same color () make up an electromagnetic wave, with wavelength . White light is then made up of equal numbers of photons of all wavelengths.
Photons have energy but no mass. Quantum mechanics describes the energy, E, of a single photon with wavelength, as
= h Where h is known as Planck's constant (h = 6.63 x 10-34 Joules*seconds, 1 Joule = 1 kg*m2/s2)
So shorter wavelength radiation has more energy than longer wavelength radiation. X-rays are more energetic than Microwaves.
Brightness (intensity): a measure of the amount of energy being received by an observer. Can be thought of as the number of photons (the greater the number the greater the brightness) or the amplitude of the electromagnetic waves.
A Spectrum of the Planet Mars.
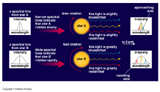
In order for an electron to make a transition from one level to the other it must change its energy by an amount equal to the difference in the levels.
When an electron drops from a higher level to a lower level it must conserve energy. It must give up some energy, the amount being equal to the difference in the two energy levels. How does it do that? Electromagnetic radiation. The electron accelerates during the transition, which creates an electromagnetic wave as described earlier. The wave is a photon, whose energy is exactly equal to the difference in the energy levels, E = hc/. And so the wavelength (color) of the light emitted is dependent on how much energy it lost in the transition. The more the energy difference the shorter (bluer) the wavelength. This process is called Emission.
An electron can jump up to a higher level if it can absorb a photon with just the exact energy (ie wavelength) equal to the difference in the two energy states. This process is called Absorption.
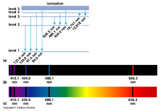
Molecules may also absorb and emit light of specific energies that correspond to discrete states of rotation and vibration.
Note: Transmission and Reflection occurs for light that does not have the specific energies needed for energy state transmissions in atoms, ions, and molecules.
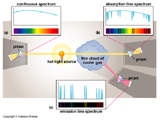
The process of absorption and emission produce rather distinctive spectra.
If you are looking at a diffuse gas of helium with a device that spreads light into its constituent colors (i.e. a prism, called a spectrograph) you will see colored lines rather than a full rainbow. These lines correspond to the wavelengths of the photons emitted by the atoms in the gas as the electrons fall from higher (excited) energy states to lower states in the helium atoms. Because the electron can only occupy specific and finite energy states there can only be a finite and specific number of lines produced by the gas. This is known as an Emission Spectrum.
Every single, atom, ion, isotope, and molecule has a unique pattern of emission spectrum -- It's a finger print for matter! So we can identify which chemical elements and molecules are present in a diffuse gas by the emission lines it produces.
A couple of things can cause an electron to be in an excited state:
If you view the light of a continuous spectrum after it has passed through a diffuse and cold gas cloud something interesting will happen. The atoms in the gas cloud will absorb certain wavelengths of light corresponding to the energy levels within the atoms. The continuous spectrum when viewed through a spectrograph will then look like the rainbow with dark lines eaten out of it where the gas cloud has absorbed photons. This is called an Absorption Spectrum. We can use absorption spectra to figure out what elements are in the intervening gas cloud.
The Energy Spectrum is a plot of the intensity of radiation vs. wavelength. So this tells you how many photons are being emitted (or received) at each wavelength. For thermal radiation the resulting curve is well understood.
The shape of the curve depends only on temperature. There is a simple relationship between the Temperature (measured in Kelvins) of thermal emitters and the peak of their energy spectrum. It is known as Wien's Law:
peakT = 2.898 x 10-3 m*K This says that the wavelength (color) where the curve peaks is inversely proportional to the Temperature. As the temperature increases the peak moves to shorter wavelengths of radiation. And so we see the color of the object change as it is heated or cools. When you turn on the burner of an electric oven it starts out glowing a red color and as it heats up goes from red to orange to yellow. The burner is emitting radiation even before you first see it glow red. It starts out emitting IR radiation because it's temperature is initially around 300 K
peak = 2.898 x 10-3 m*K/(300 K) = 9.7 x 10-6 m
No object is perfectly opaque (absorbing and re-emitting all light that falls upon it), but most of the objects we'll encounter in this class will approximate perfect thermal emitters.
Two rules to remember about thermal radiation:
Objects in motion compress the light waves in front of them making them appear more blue (blue shift), the light waves behind are stretched out and appear more red (red shift).
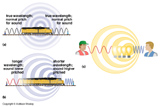
Amount of shift of wavelength is proportional to the component of velocity along the line of sight.
Can calculate the velocity of motion along the line of sight:
/0 = v/c
Where c is the speed of light, 0 is the wavelength of the light as seen at rest, and is the measured change in wavelength.
This is extremely important in astronomy. We can measure the velocities of stars with respect to us. We can measure their rotational velocities. We can measure their speeds of orbit in binary systems. Plus we can measure their change in velocity caused by a planet in orbit around them.
We characterize the brightness of an object as some number of photons being collected per unit area per unit time. Brightness is therefore the amount of radiation received by us. We cannot change how bright an object is. But we can change the number of photons we collect.
We Can...
For human eyes the collecting area is only the total area of your two pupils. It's not very big. Furthermore, your eyes only collect light for about 1/30th of a second before they send the info to your brain and start collecting again (like frames of a movie). That's why when you look through a telescope at, say the Orion nebula, it does not look as impressive as it does in the pretty pictures in text books. Plus we cannot record precisely what our eyes saw and study it later quantitatively. So, we need telescopes...
We typically rate telescopes by the size of their collecting area. Since the collecting areas are usually circular we describe them in terms of their diameters:
A typically large telescope has a diameter of Dt = 4 m, whereas your dilated eye has a diameter of about De = 4 mm (4 x 10-3 m).
R2 = D2/4 , since R = D/2Ratio of areas:
At/Ae = ((4 m)/(4 x 10-3 m))2 = 1 x 106
The secondary purpose of a telescope is to provide greater resolution
Resolution is the ability to detect fine detail. For example, the bright star in the bend of the handle of the Big Dipper, Mizar, looks like just one star to your eye. But in a telescope it is revealed to be two stars. Your eye cannot resolve angles small enough to separate the two stars in the image on your retina.
This is is because of a wave property that light has called diffraction. As a wave passes through an aperture the planar wave is converted into a spherical wave as seen in the following figure:
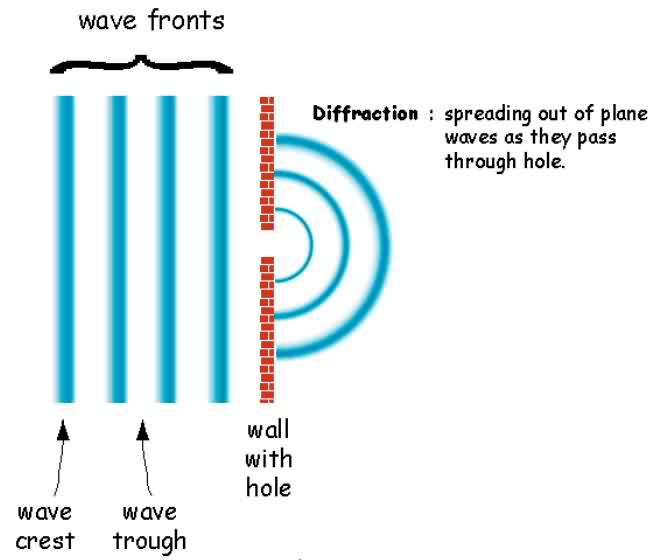
In a telescope (or your eye) which has a circular aperture this leads to point sources being surrounded by rings of light. When the rings of one point source overlap the rings of another it becomes impossible to discern one point source from the next.
, that a circular aperture, with a diameter D, can resolve for light with wavelength .
1.22/D
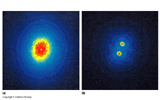
What is the diffraction limit of the Keck telescope in Hawaii? It has a diameter of 10 m. It is an optical telescope, so let's use the middle wavelength of the optical spectrum as the fiducial wavelength, = 5500 Å.
1.22(5500 x 10-10 m)/(10 m) = 6.7 x 10-8 radians * 206,265"/radian = 1.4 x 10-2" = 14 milli-arcseconds (mas)
The Keck Telescope does not actually achieve this small of an angle, however. The atmosphere blurs the light of any incoming point source and spreads the light out over a larger angle than the diffraction limit of the telescope.
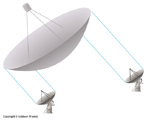
Some radio telescopes are used in arrays called interferometers. These arrays observe radio waves and very carefully time their arrival. They then correlate the signals from each dish to put together an image. The result is that the array has the effective diffraction limit of a telescope with the diameter equal to the span of the the array. An international union of radio observatories has managed to use radio telescopes from all over the world to make observations that have the effective diffraction limit of a radio telescope the size of the Earth!
Today, we no longer use photographic plates. We now use CCDs (Charged-Coupled Devices). They are solid-state semi-conductor chips that work on the principle of the photoelectric effect discovered by Einstein. Photons can knock electrons loose when they collide with certain elements. These loose electrons created a charge that we can measure. CCDs are used in video and digital cameras. Science grade CCDs have arrays of pixels of 2048 x 2048 or more. Each pixel stores electric charge in direct proportion to the amount of light that has been incident upon it.
CCDs have many advantages:
Return to Class Notes Page