Astronomy 10: Lecture 7

Lecture 7

Thursday, June 6th 2002. Reading: Cosmic Perspective Chapter 5

Isaac Newton (1642 - 1727)

Isaac Newton was born in an English village the year that Galileo died. His were very humble beginnings, and yet he would rise to become arguably the greatest scientist the world has ever known. He was a sickly, quarlesome, and unsocial individual. It has been rumored that he remained a virgin until the day he died.

When he was 20 years old he bought a book on astrology at a fair, "out of curiosity to see what was in it." He came upon a figure in the book that he did not understand because it involved trigonometry and he was ignorant of trigonometry. So he bought a book on trigonometry. When he couldn't follow the geometrical arguments in that book he bought himself a copy of Euclid's Elements of Geometry. Two years later he invented differential calculus.

In 1666 he was an undergraduate at Cambridge University when an outbreak of plague forced him to spend a year away in the isolated village of Woolsthorpe, where he had been born. In that year he invented differential and integral calculus, made fundamental discoveries on the nature of light, and began to think on the law of Universal Gravitation. It was quite a year.

Mechanics

Velocity and Acceleration

Speed: Time rate of change of position.

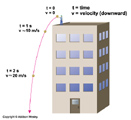
Velocity: Speed in a specific direction. Velocity is specified by a Vector. It has both magnitude and direction.

Acceleration: The time rate of change of velocity (speed and/or direction). Acceleration is also a vector.

Momentum and Angular Momentum

Momentum: The combination of both mass and velocity. Example: "A 1 ton truck moving 60 mi/hr due North." Mathematically: p = mv Momentum is a vector, and it always conserved (can be neither created nor destroyed, only transfered).

Angular Momentum: momentum of spinning/rotating or revolving. It is also a vector and is also conserved. Mathematically:

L = mv x r Here the quantity r is the radius of angular motion (radius of an orbit, size of a spinning object).

Force and Torque

Force: "Push/Pull" - The time rate of change of momentum. It is a vector quantity. Mathematically:F =

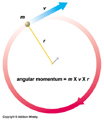
Torque: The time rate of change of angular momentum. Also a vector. Mathematically:

= F x r

Newton's Laws of Motion

In 1687 Netwon finally published his Principia were he laid out his laws fundamental laws of motion.

The Law of Inertia: If the sum of the forces on an object add to zero then the object's velocity will remain constant.
- "An object in motion tends to stay in motion, and an object rest tends to stay at rest."
- do nothing to an object and it will keep doing what it has been doing all along.
- inertia is the idea that an object will resist a change in its motion (either making it move or trying to stop it from moving).
Note: since neither speed nor direction of motion changes that we always have motion in a straight line when there are no forces.
F = ma
- acceleration experienced by an object is directly proportional to the amount of force exerted on it.
- The constant of proportionality is the object's mass.
- This is how mass is essentially defined. Sometimes it's refered to as inertial mass.
Action and Reaction:
When two bodies interact, they create equal and opposite forces on each other. (Examples: Two gravitating bodies exerting the same gravitational force on each other, two skateboarders pushing on one another, a ball bouncing off the wall, astronaut throwing a hammer, etc...)

Circular Motion

The law of inertia tells us that if there are no forces acting on an object then its motion is in a straight line. So how do we produce circular motion, like that of the planets in their orbits?

We have to apply a force. The force that we need to apply must constantly change the direction of of the object's motion without altering the tangential speed of the object. We can show this with an object tied to the end of a string. If we swing the object around in a circle above our heads the force that is causing the object to go around is the tension in the string. You can feel the tension as you swing the the object. If we were to suddenly cut the string the object would continue off on a tangential line from the spot it was released. It will not continue on in a curved path.

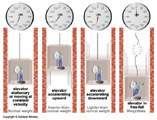
The force that keeps planets, moons, etc. in orbits is gravity, the natural attraction of all matter to other matter. We can visualize how to put something in orbit by imagining firing a canonball from a very high mountain. The greater the initial velocity we give the ball the farther down range it will go before falling to the Earth. If we get it at just the right speed it will continue to fall toward the Earth, but the Earth's curvature will continue to curve away from it and it will make a full circle and eventually hit the back end of the canon.

So an object in orbit is indeed experiencing gravity. For example the Space Shuttle when it is in orbit around the Earth is always falling toward the Earth, but it is also heading tangentially at just the right speed to stay in a circle (or ellipse). So it is always under the influence of gravity. The astronauts appear weightless because they and the Shuttle are all falling together at the same rate.

The Universal Law of Gravity

Newton made the connection between the "magnetic" force that Kepler had supposed caused his 2nd law implied and the everyday force of gravity. The old story goes that one day Newton was out sitting under an apple tree looking at the Moon. The story goes that when he saw an apple fall he wondered if the force that was keeping the Moon in orbit around the Earth was the same force that made the apple fall to the ground. That would mean that the Moon is always falling toward Earth in the way we described above. He also then reasoned that it must be gravity that holds the Earth and planets in orbit about the Sun. So we are always falling toward the Sun.

He studied Kepler's 3rd law of planetary motion and his own laws of motion to come up with a Universal Law of Gravitation. Given two masses, m₁ and m₂ the force between them is given by

F = - Gm₁m₂/r² Where r is the distance between the two objects and G is a constant found empirically, G = 6.67 x 10^-11 m³*g^-1*s^-2. By Netwon's 3rd law this is the force felt by both objects. The negative sign indicates that the force is attractive it draws the two bodies together.

For example the force of attracttion that your body feels toward the Earth is the same force of attraction that the Earth feels toward you. But since Earth is way more massive than you its acceleration is much, much, much less than yours. You can see this by relating the law of gravitation to Newton's second law.

F = - GMm_you/r² = - m_youa_you = -Ma So your acceleration toward Earth is a_you = GM/r² And the Earth's acceleration toward you is a = Gm_you/r² And so the ratio of Earth's acceleration to yours is a/a_you = m_you/M Which is a very small number. And so Earth doesn't react much to your presence, but you react alot to Earth's.

Kepler's 3rd Law

Netwon also found that he could derive Kepler's 3rd law using his new fangled-dangled invention: calculus. In doing so, he realized that he could figure out what that constant of proportionality was in Kepler's 3rd Law. It turns out that it depends on the masses of the two objects in question. He found the general form to be P² = 4

²/G(m₁ + m₂) * a³ So the constant k = 4

²/G(m₁ + m₂).

IMPORTANT: If m₂ << m₁ then we may ignore m₂ such that m₁ + m₂ m₁ then the relation becomes

P² = 4

²/Gm₁ * a³ This is the case for all the planets in the solar system compared to the mass of the Sun and likewise for most of the moons in the solar system compared to their mother planets.

This fact can be used to measure the mass of the Sun. For all planets in the Solar System we may write

P² = 4

²/GM * a³ Let's rearrange the equation in the usual way to isolate the quantity that we want to know. M = 4

²/G * a³/P² We know all these values for Earth and if we plug them in we find that M = 2 x 10³⁰ kg

Surface Gravity

Newton spent many extra years thinking about a certain problem involving the gravity of a spherically symmetric mass. He believed that the body would behave as though all of its mass was concentrated at the center. But in order to prove this he would need to invent integral calculus. Indeed his intuition was correct.

That means if you have mass, m, and are standing on the surface of a planet with Mass, M, and Radius, R, then the force of gravity acting on you is

F = -GMm/R² .

Now notice also that it is true by Newton's 2nd Law that

F = -GMm/R² = ma Simplifying the expression... a = -GM/R² This says that the acceleration you feel due to the planet is independent of your mass. That's just what Galileo showed in his famous experiment of dropping canon balls from the leaning tower of Pisa.

NOTE: the force you feel due to gravity is your weight

Escape Velocity

If you wish to escape from the surface of a gravitating object there is a special velocity you must have in order to accomplish this. It's called the escape velocity. The best way to understand this is to think in terms of energy. In order to be able to escape from a planet you want to have an initial velocity that will make your total mechanical energy be at least zero or greater (unbound). Recall that the total mechanical energy is written as

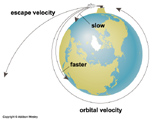
E = KE + PE In our initial system we have KE = 1/2 mv_esc², and PE = -GMm/R. We want E to at least be equal to zero to be unbound. So we may then write E = 1/2 mv_esc² - GMm/R = 0 Let's now solve this for the escape velocity. 1/2 mv_esc² = GMm/R So, again we see that the mass, m, of the object is unimportant to the calculation. v_esc = (2GM/R)^1/2

An interesting idea that was raised not long after Newton's time was that if an object were to have just enough mass enclosed in a small enough radius the escape velocity would be greater than the speed of light, and then not even light could escape the surface of this object. It was then known as a "Black Star". Today this is rather similar to the idea of a Black Hole.

Planetary Orbits

Planetary orbits were found by Kepler to be ellipses. But Newton found that they are even more general than ellipses, they are conic sections.

Another way that these curves are thought of in relation to one another is in terms of eccentricity; it's the measure of the amount of squashiness a conic section has. A conic section with an eccentricity, e = 0, is a circle, 0 < e < 1 is an ellipse, e = 1 is a parabola, and e > 1 is a hyperbola.

The conic section that an orbit will exhibit depends on its total energy. If the total energy of the system is negative then the orbit is bound and is an ellipse. If the energy is exactly equal to zero then it is unbound and follows a parabolic shape. If the energy is positive, then the orbit is unbound and follows a hyperbola. This is summed up in the following table...

Energy Bound/Unbound Shape Eccentricity

E < 0, minimum Bound Circle e = 0

E < 0 Bound Ellipse 0 < e < 1

E = 0 Unbound Parabola e = 1

E > 0 Unbound Hyperbola e > 1

Tides

Because the force of gravity is weaker with increasing distance the gravitational pull an extended object will feel will be different across its length. This differential gravity is called a tidal force.

The Moon exerts a differential pull on Earth and this is the cause of the tides on Earth.

The side closest to Earth is accelerated toward the Moon the most
the center a little bit less
and the far side of Earth less still.

This causes the shape of Earth to be squished out like a football.

Since the rock of Earth is less likely to distort, the oceans do most of the distorting. High tide occurs when the Moon is overhead or at the nadir of its overhead position. Likewise, low tide is when the Moon is 90° from overhead. There are two high tides and low tides every day.

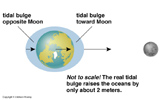
The Sun also contributes to this, but the Sun's tidal distortion on Earth is half that of the Moon's because of its distance. The maximum tides occur when the Earth, Sun, and Moon are all in a line (new and full Moon). The minimum tides occur when the Moon is in either quarter phase.

This process causes a kind of friction that slows the Earth's spin. In doing so Angular momentum must be conserved and so the Moon's orbital angular momentum increases and it moves farther away.

This friction is a kind of energy loss of the system. The energy loss continues until a minimum amount of friction is present. The Moon was likely spinning faster on its axis, but the Tides raised on it surface by Earth slowed it into lock-step with its orbit. This is called orbital resonance. It is a minimum energy loss state.

The Earth will one day reach a similar state. Then the day will be as long as a month, which will also be longer than the current month because the Moon will be farther away. The Moon's angular size in the sky will be smaller and there'll be no more total solar eclipses. Also Earth will show only one face to the Moon just as the Moon currently does to Earth.

This will actually never happen because the Sun will die out and destroy Earth first.

Return to Class Notes Page

Energy	Bound/Unbound	Shape	Eccentricity
E < 0, minimum	Bound	Circle	e = 0
E < 0	Bound	Ellipse	0 < e < 1
E = 0	Unbound	Parabola	e = 1
E > 0	Unbound	Hyperbola	e > 1