Astronomy 10: Lecture 4
Lecture 4
Monday, June 3rd 2002. Reading: Cosmic Perspective Chapt. S1 and 3
Time Keeping
- 1 Day = 1 Diurnal Cycle of the Sun = 24 hours ~ 1 rotation of the Earth
- 1 Month = 1 Synodic Cycle of the Moon. ~ 30 days ~ 1 revolution of the Moon
- 1 Year = 1 Revolution of Earth about the Sun = 365.25 days

The Solar Day on Earth is in fact a Synodic Day. The Mean Solar Day is defined as the time it takes the Sun to transit the meridian twice. But again during that one day Earth has moved in its orbit (about 1°) and as seen in the Sidereal frame of reference it completes one spin before the Sun can again be in position to transit. The Synodic Day is defined as 24 hours. The Sidereal day, the actual time it takes Earth to complete one spin and the time between consecutive transits of any given star is about 23 hours and 56 minutes. It's 4 minutes shorter. This leads to there being 366 Sidereal days in a year. It also means that stars rise and set each day 4 minutes earlier than the previous.

Celestial Navigation: The Sky from different places on Earth
The Appearance of the Daily Motions of the Sky depends upon where you are on Earth.
First We examine the paths of Stars from several locations on Earth:
The North Pole 
The Equator 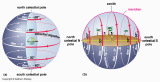
40° N 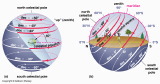
30° S 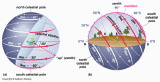
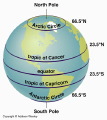
The path of the Sun through the sky changes not only with position on Earth, but also with the time of the year. This is due to the 23.5° tilt of Earth's rotation axis to its orbital plane.

The North Pole 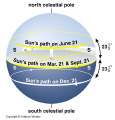
The Equator 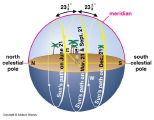
The Tropic of Cancer 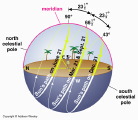
The Arctic Circle 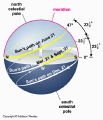
The Shape and Size of Earth
- What is the Shape of the Earth?
- Looks Flat
- The closer to Earth's Surface you get the more and more you cannot discern the curvature and it looks flat.
- Evidence for Curvature
- As ships head out to sea they don't disappear all at once, but rather their masts disappear last.
- The Sun's position in the sky is different from different locations on the same day.
- As you move north or south you can see different stars that were previously hidden by the horizon. Not possible on a flat Earth.
- Evidence for Spherical
- The Moon and the Sun are circular in projected appearance (the Moon's Phases give away its spherical shape), Why not Earth?
- Earth's shadow on the Moon during a lunar eclipse is circular. Eclipses happen at all altitudes so Earth must be Spherical (Aristotle ~300 B.C.)
- What is the size of Earth?
- Eratosthenes figures it out.
- Reads a report about the Sun being seen at the bottom of a well and no shadows being cast at noon on the Summer Solstice in Syene.
- He never observed this to happen in Alexandria.
- Must be due to Earth's curvature.
- Meausure the angle of the shadow made by objects in Alexandria, on June 21st: 7°
- Measure the distance between Alexandria and Syene: 500 Stadia = 800 km (hires a man to pace this out)
- The ratio of the angle to that of a full circle would be equivalent to the ratio of the distance between Alexandria and Syene and the Circumference of the Earth: 40,000 km.
- Real Answer: 40,030 km
- Wow!!!

The Measurements of Aristarchus of Samos
Distance and Size of the Moon
In the 3rd Century B.C. (about 75 years before Eratosthenes), a great Greek thinker figured out a way to measure the relative sizes and distances of the Moon and Sun. His name was Aristarchus of Samos (circa 310 - 230 BC).
These calculations involve some straightforward logic and the application of simple geometry.
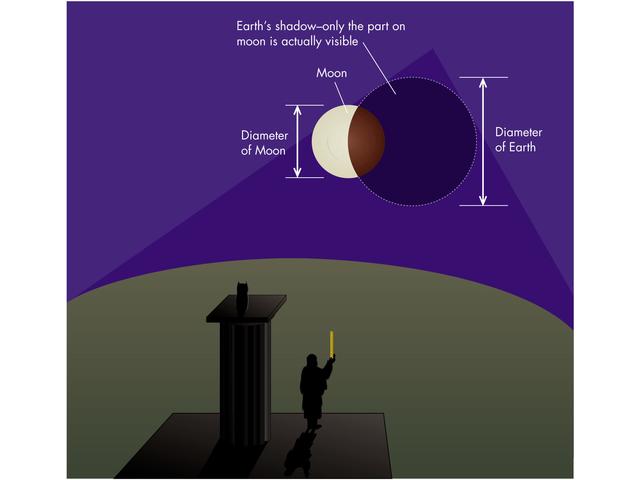
The first thing that Aristarchus noticed was that when the Moon was eclipsed by the Earth you could see the Earth's shadow creep across the face of the Moon. Earth's shadow is circular, and if you assume that the Sun's rays are roughly parallel to one another that implies that the size of Earth's shadow at the distance of the Moon is equal to the size of Earth. It's not exactly true, but it's very close. From the arc of Earth's shadow you can estimate the size of it's full circle, then you measure the size of the Moon's circle. This tells you the relative size of the Earth to the Moon. What you are measuring is the angular size of the Earth's shadow and the Moon. In the limit of small angles, physical size and angular size are directly proportional.
Aristarchus measured a ratio of Earth's size to the Moon's size to be:
D /DM = 2.86
(Where the symbol
/DM = 2.86
(Where the symbol  refers to Earth)
refers to Earth)
The real answer is 3.67. So the Moon is about one-third the size of Earth.
Using the angular size of the Moon we can estimate its distance as well using the relationship between angular size ( ), physical size (D), and distance (d):
), physical size (D), and distance (d):
 = D/d
Where
= D/d
Where  in this equation is in radians, the natural, unit-less measure of angles. The conversion from radians to degrees is simply:
2
in this equation is in radians, the natural, unit-less measure of angles. The conversion from radians to degrees is simply:
2 radians = 360°
radians = 360°
-> 1 radian = 57.3°
The angular size of the Moon is about 0.5° ( = 0.5°). Thus we have a distance to the Moon of about 30 Earth Diameters (dM = 30D
= 0.5°). Thus we have a distance to the Moon of about 30 Earth Diameters (dM = 30D )
)
Distance and Size of the Sun

Next Aristarchus reasoned that when the Moon was seen to be exactly in either 1st or 3rd Quarter Phase (exactly half lit up as seen from Earth), we can draw a right triangle between Earth, Moon, and Sun. The legs of the right triangle are the distance from the Earth to the Moon (dM) and the distance between the Moon and the Sun (dM ). The hypotenuse is then the distance between the Earth and Sun (d
). The hypotenuse is then the distance between the Earth and Sun (d ). (The symbol
). (The symbol  refers to the Sun). We can measure the angle between dM and d
refers to the Sun). We can measure the angle between dM and d (
(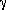 ), it's the angular separation between the Sun and Moon in the sky. Once again a little simple trigonometry then gives us the distance to the Sun.
), it's the angular separation between the Sun and Moon in the sky. Once again a little simple trigonometry then gives us the distance to the Sun.
Aristarchus measured 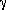 = 87°. This corresponds to a distance to the Sun of d
= 87°. This corresponds to a distance to the Sun of d = 573D
= 573D . Now, the angular size of the Sun is also about 0.5° so by the same method as for the Moon Aristarchus estimated that the Sun was 5.33 times bigger than the Earth.
. Now, the angular size of the Sun is also about 0.5° so by the same method as for the Moon Aristarchus estimated that the Sun was 5.33 times bigger than the Earth.
This measurement is a difficult one to make, and the real answer is 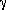 = 89.9°. This corresponds to a distance to the Sun of d
= 89.9°. This corresponds to a distance to the Sun of d = 11,700D
= 11,700D and a size of the Sun, D
and a size of the Sun, D = 109D
= 109D .
.
Either way, Aristarchus was able to establish that the Sun was bigger than Earth. Since this was so, he reasoned that it would make more sense for Earth to orbit the Sun rather than the other way around. But his contemporaries pointed to some arguments of Aristotle's that contradicted such an idea. One critical one being that the stars should exhibit parallax if Earth goes about the Sun. They do indeed exhibit this phenomenon but they are so far away that it cannot be measured without a telescope. It would be some 1900 years before Aristarchus would finally be proved correct by the work of Kepler and Galileo.
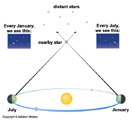
Motion of the Planets in the Sky
- After you observe the sky long enough you will notice that there are few special "stars". They do not twinkle like the other stars, and they do not keep the same annual rhythms.
- These were known as the wanderers by the Greeks, or Planets.
- There are 5 naked eye Planets: Mercury, Venus, Mars, Jupiter, and Saturn. Named after the Olympian Gods of classical mythology. The planets Uranus, Neptune, and Pluto were not discovered until well after the invention of the telescope.
- Days of the week are names after the wanderers:
- Sunday: The Sun
- Monday: The Moon
- Tuesday (martes): Mars
- Wednesday (miercoles): Mercury
- Thursday (jueves): Jupiter
- Friday (viernes): Venus
- Saturday: Saturn
- The planets are known as wanderers because they change their positions with respect to the stars but all with different periods.
- The planets all wander through the Zodiac. They do this because all of the planets in our solar system orbit the Sun in a plane. Their individual planes are all a tiny bit different from ours. So as seen from Earth they will all be very close to the ecliptic plane (Earth's orbit). If they were all in exactly the same plane they would all lie exactly on the ecliptic.
- The planets' motions are sufficient slow that you need to watch over the course of several days/weeks/months to notice them. So they still always rise in the East and set in the West.
- Their general motion through the Stars is from West to East. This is because they are all orbiting the Sun in the same direction as Earth is.
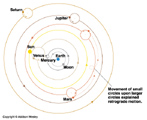
- Occasionally they move East to West through the stars for a few months. This is called retrograde motion. The planets do not actually change their directions in their orbits. Rather it's an optical illusion caused when Earth passes the planet by.
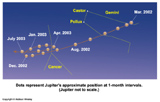
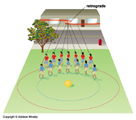

- The majority of ancient Greek thinkers prefered a model of the Universe with the Earth at the center: Geocentric.
- Ptolemy devised the best geocentric model which accurately explained and predicted planetary motion. Used Epicycles to explain retrograde motion. The model stood for 1500 years.
The History of Astronomy
Early Timeline
Ancient Astronomy
- ~17,000 BC, Lascaux cave paintings depicting celestial events
- Egypt
- The Pyramids built with celestial alignments accurate to within a few minutes of arc.
- Used Diurnal Motions as a clock
- Babylonia
- Developed sexagesimal (60) counting system: 360 degrees in circle, 60 minutes per hour, 60 seconds per minute, etc.
- Compiled tables of planetary motion
- Predicted eclipses
- No understanding of why events occurred, no pictures of orbits, no geometry!
- China
- Well-preserved historical records dating back 3000 years
- Oldest records of comets, eclipses, sunspots, etc.
- Astronomy tied to political bureaucracy and functioning of government
- Decline in the importance of Astronomy after 1200 AD
- Mayans
- Developed a complicated and extremely accurate calendar
- precise tables of for motions of Moon and Venus
- predicted eclipses
All cultures on Earth have made some understanding of the motions of the heavens. But the contribution by the Greeks of the use of a scientific reasoning was special and led to great discovery.
The Greek Contribution
- Pythagoras of Samos (circa 580 - 500 BC)
- Mystical understanding of the Cosmos using mathematics
- Numbers as a bridge between humans and the divine mind
- Invented the roots of the western musical scales
- Believed in a spherical Earth, by reasoning alone and not with any evidence whatsoever.
- Postulated that Sun, Moon, and planets move in concentric circles
- Believed the distances were in ratio with musical harmony: Music of the Spheres
- Plato (circa 428 - 348 BC)
- Student of Socrates (c. 470 - 399 BC)
- Ascendency of the role of deductive reasoning.
- Believed sensory experience to be subjective, that pure thought was preferable to experiment.
- Urged astronomers to think about the heavens, but not to waste their time observing them.
- Philosophy was the work of the mind
- Manual Labor was for slaves
- The Physical World is merely a shadow of the perfect world of the forms
- The Pythagorean solids and their correspondence to the 5 Elements:
- Fire - tetrahedron (4 sides, triangles)
- Earth - cube (6 sides, squares)
- Air - Octahedron (8, triangles)
- Water - Icosahedron (20, triangle)
- Cosmos - Dodecahedron (12, pentagons) : knowledge of this shape suppressed by Pythagoreans
- Eudoxus (circa 408 - 356 BC)
- Devised a model of the Universe as an answer to a challenge put forth by Plato.
- Universe consisting of nested spheres with the planets attached
- Retrograde Motion a result of planets being attached to smaller spheres affixed to the larger spheres: epicycles
- Aristotle (384 - 322 BC)
- Student of Plato's Academy
- Worked in almost every field of known science and philosophy!
- Believed that every effect has a cause
- Important innovation: Universe can be described by natural laws inferred by rational thought
- Invented a system of Physics: mostly quite wrong, but had a strong common sense appeal - suffered from lack of experiment in some cases (Pythagorean bias)
- Founded science of mechanics (physics of motion)
- developed the idea of force, impetus theory of motion (wrong, but still widely held even today)
- Thought force was required to keep a body in motion
- Separate laws for Earth and the Heavens
- Gravity on Earth but not in Heavens
- Natural motion is straight lines on Earth, circles in Heaven
- Reasoned that Earth was spherical based on observations of Earth's shadow on the moon, the fact that different stars can be seen farther south than Greece, etc.
- Believed in a Earth-Centered Universe with the Heavens rotating above - Geocentric
- Heraclides (circa 388 - 310 BC)
- Proposed that Earth is rotating to explain the daily motions of the heavens.
- Proposed that Mercury and Venus orbit the Sun because they never get very far from the Sun
- His ideas were soundly rejected by the Aristotle school of thought
- Aristarchus of Samos (circa 310 - 230 BC)
- Measured the relative sizes and distances to the Moon and Sun
- Found the Sun to be Bigger than Earth!
- Reasoned that the Sun rather than Earth is the center of the Universe and the Earth is one of the planets
- His ideas again rejected by Aristotle, no parallax of stars
- Eratosthenes of Cyrene (276 - 194 BC)
- Director of the Library of Alexandria
- Read an account of the Sun's path on the Summer Solstice in the southern frontier city of Syene.
- He realized that Earth must be curved and correctly calculated its size
- Hipparchus of Rhodes (190 - 120 BC)
- Synthesized Babylonian and Greek data with new Greek geometrical models
- Constructed the largest star catalogs in existence at the time
- Discovered the precession of Earth's axis
- Refined Aristarchus' measurements
- Measured the length of the year to an accuracy of 6 minutes!
- Devised a system of brightness for the stars: magnitudes: still in use today (much to the chagrin of modern astronomers)
Ptolemy (circa 140 AD)
Claudius Ptolemaeus, a.k.a Ptolemy, was also a director of the Library of Alexandria in his time. He is sometimes considered the last great natural philosopher of classical times. (I would argue however that this identification falls to the last director of the Library of Alexandria, Hypatia, who was brutally murdered by a Christian lynch mob in 415 AD.) He put together a model of the Universe that did not change much for 1500 years. Ptolemy used the collected observations of Hipparchus to build his model and to measure the parallax of the Moon, and thereby make another measurement of its distance.
His model was marked by using the geocentric model first developed by Eudoxus. He considered a heliocentric model, like that proposed by Aristarchus, but immediately rejected it based on Aristotelean physics. He made alterations to the geocentric model, added some epicycles within epicycles in order to make the model explain all of Hipparchus' data. He also offset some of the spheres so that they were not necessarily concentric with Earth. The most important thing about this model was that it was able to predict the positions of the planets with great accuracy (at least to the level that people were able to measure in those times). The model contained no explanation for how or why these motions occurred (it had no physics).
In subsequent centuries the alterations made to the model would be to add more epicycles into the model. This was done primarily by Arabic astronomers in medieval times. In the end some planets would have as many as 80 epicycles in order to be able to properly predict where they would be.
Ptolemy also codified the pseudoscience of astrology into the form which is still in use today. That just goes to show that great genius is no guarantee against being dead wrong.
Return to Class Notes Page


















![]() ), physical size (D), and distance (d):
), physical size (D), and distance (d):

![]() = 87°. This corresponds to a distance to the Sun of d
= 87°. This corresponds to a distance to the Sun of d![]() = 573D
= 573D![]() . Now, the angular size of the Sun is also about 0.5° so by the same method as for the Moon Aristarchus estimated that the Sun was 5.33 times bigger than the Earth.
. Now, the angular size of the Sun is also about 0.5° so by the same method as for the Moon Aristarchus estimated that the Sun was 5.33 times bigger than the Earth.![]() = 89.9°. This corresponds to a distance to the Sun of d
= 89.9°. This corresponds to a distance to the Sun of d![]() = 11,700D
= 11,700D![]() and a size of the Sun, D
and a size of the Sun, D![]() = 109D
= 109D![]() .
.




