Thursday, June 27th 2002. Reading: Cosmic Perspective Chapters 20 and 21
d2b.
Find that some galaxies have extremely luminous center (nucleus). "Active". Radio, X-rays, UV, Optical, ... Quasars are related.
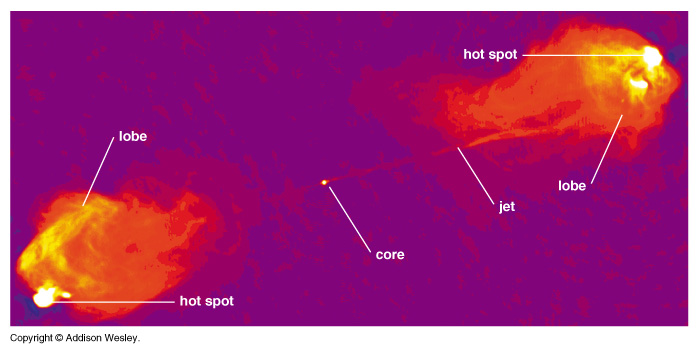
"Radio Galaxies": Often 2 lobes of radio emission, far from nucleus. Jets of particles and radiation shot out of nucleus: over 1 Mpc in size!
Gas in active galactic nuclei (AGN) often has huge speed (> 104 km/s). Stars probably NOT responsible for activity.
Quasars (quasi-stellar radio sources)
Radio Astronomers had been trying to get better and better
positions for radio sources, to try to find out what they were.
Development of radio interferometry made it possible to get
accurate positions.
In 1960, certain stars were found to be associated with two
of these radio sources, but the stars have very strange spectra.
Different quasars had different spectral lines in different places!
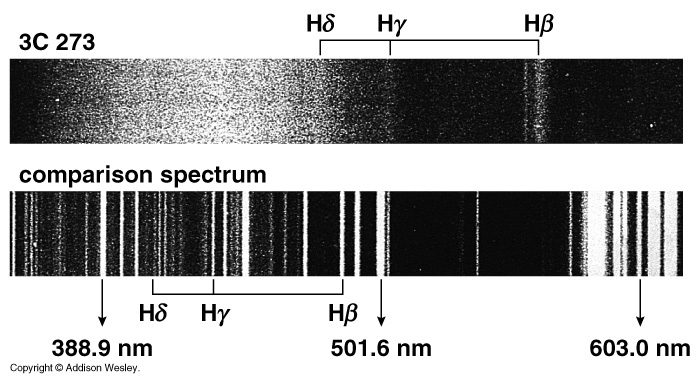
In 1963, Maarten Schmidt and Jesse Greenstein of Caltech realized that 3C 273 has basically the spectrum of hot (10,000 K) hydrogen, redshifted by 16%! (z = 0.16) That's a huge redshift! Other quasars had even higher z!
If the redshift is due to expansion of the Universe, the quasars must be very far away.
/o = v/c --> 48,000 km/s. Extremely distant, but much brighter (100 - 1000 times) than galaxies with the same redshift (i.e., distance). Extremely large Luminosity!
NOTE: "Radio quiet" quasars were subsequently found. Sometimes called QSOs (quasi-stellar objects). Tend to use the terms interchangeably.
The next surprise: variability
Brightness of some quasars varies dramatically over months or years (some: weeks). Therefore, light-emitting region is not larger than a few light-months or light-years!
For an object that is about 1 light-year in diameter it would take at least 1 year for the brightness, as seen by a distant observer, to vary, even if the intrinsic variation occurs instantaneously throughout the object.
Thus, quasars are very small (relatively) yet release tremendous amounts of energy!
What produces so much energy in such a small volume? Nuclear Energy? - Nope. Regis Philbin? - Nope.
By process of elimination we come to one conclusion: HUGE BLACK HOLES (MBH = 107 - 109M ) in the centers of galaxies, swallowing (accreting) 1-10M of gas per year.
Matter falls and gains speed. Viscous friction in the accrection process heats the gas. Energy is radiated away before the matter is swallowed. ~10% efficiency. High speed, well focused jets of particles shoot out perpendicular to the accretion disk: due to magnetic field, etc. Radio Galaxies also do this.
|
Recently, high-quality CCD images (HST) and spectra (Keck) of relatively nearby QSOs (z = 0.2 - 0.3) show conclusively that they are at the centers of galaxies. Some are interacting or merging with other galaxies --> gas driven toward BH, and emits energy before being eaten.
|
|
Soon after the discovery of quasars, some were found with z > 1 (e.g., 2 - But this DOES NOT mean v = 2c, since v = cz works only for v/c < 0.2). Use relativistic Doppler shift: Highest known: z = 5.8 (1000 Å at 6800 Å) --> v = 0.98c. We see the QSO when the Universe was ~10% of current age!
|
The most luminous QSOs are extremely distant: few nearby. Denizens of the young Universe. What happened to them?? They probably faded with time, as the central black holes gobbled up most of the surrounding gas and dust.
Some nearby active and normal galaxies may have been QSOs in the distant past. The Milky Way Galaxy has a somewhat active nucleus. MBH ~ 4x106M |
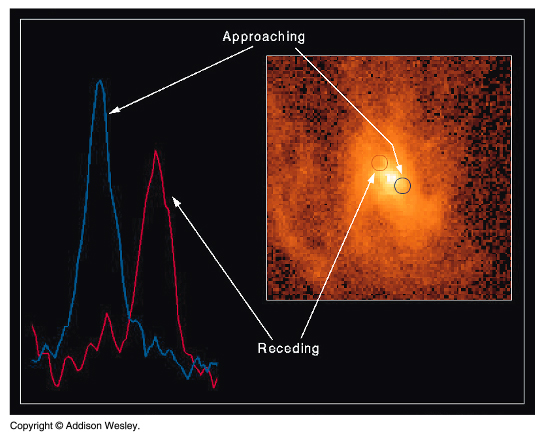
How do we know there are black holes there with these huge masses?: Recently, however, stars very close to the centers of several normal (or mildly active) galaxies (including the Milky Way) have been shown to be moving very rapidly, along with disks of rapidly rotating gas. P2 = 4 2/G(M1 + M*) * r3.
M* << M1 And just as in the case of the stars around the galaxy we find: For r = 10pc, v = 600 km/s --> M1 = 8 x 108M . Has to be a Black Hole. |
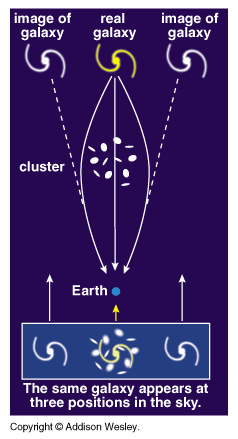
In a few cases we see two QSOs close together in the sky (just a few arc seconds apart) with identical spectra (redshift and emission lines). We can understand this as a gravitational lensing event.
Light from the QSO is bent by gravity of galaxy or cluster (warped spacetime: it's following the shortest path through the space). If had a sphere lensed by a perfectly aligned, point-like lens, would get an "Einstein Ring". This is occasionally seen; usually deviations from symmetry lead to discrete images. |
When distant galaxies (instead of QSOs) are lensed, tend to get arcs. these are seen around many rich clusters of galaxies. The clusters act as gravitational lenses. The number and distribution of arcs depends on the mass of the cluster. ---> measure total mass (luminous and dark). --> Conclude that clusters are dominated by dark matter (~90% of total mass). Yet, more evidence for dark matter. |
|
Dark Matter is found to be the major component of all galaxies. It is found by studying the rotation curves of spirals (and the deviation of velocities from the average in Ellipticals)
|
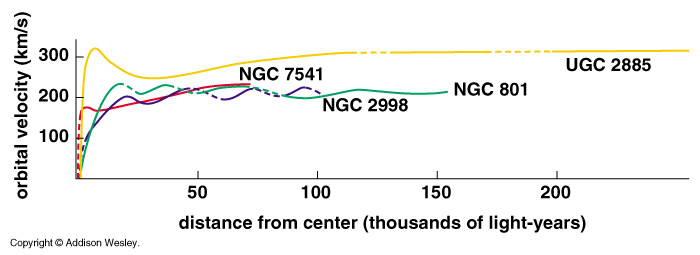
More Massive Galaxies Rotate at faster speeds. |
Analysis of the rotation curves indicates that the Dark Matter is distributed in Spherical Halos surrounding the visible portions of galaxies.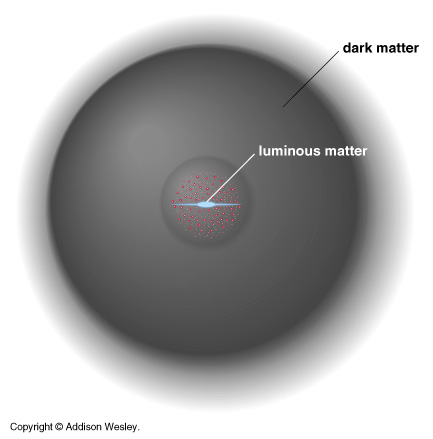
 Searches for MACHOs reveals that they do indeed exist, but not in great enough numbers to account for all the Dark Matter. Most of it must be something else. |
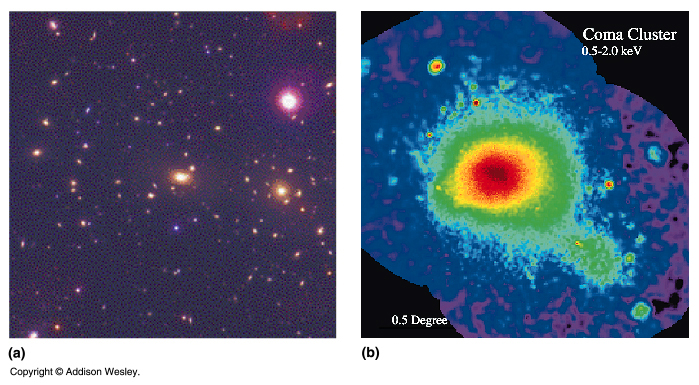
Within clusters there exists very hot gas between the galaxies (IntraCluster Medium). It is so hot that it is ionized and emits mostly X-Rays. This gas may be heated to such high temperatures by supernovas going off within the clusters' galaxies. The mass of the gas appears to be greater than the mass of stars within the galaxies of the clusters. The gas is in a kind of hydrostatic equilibrium within the cluster. Its high temperature provides a balance to the gravity of the cluster. Thus we can use the temperature (which is the measure of the average kinetic energy of the gas particles) to estimate the mass of the cluster. We find that within the cluster Dark Matter is again the most dominant form of matter by about 90%. |
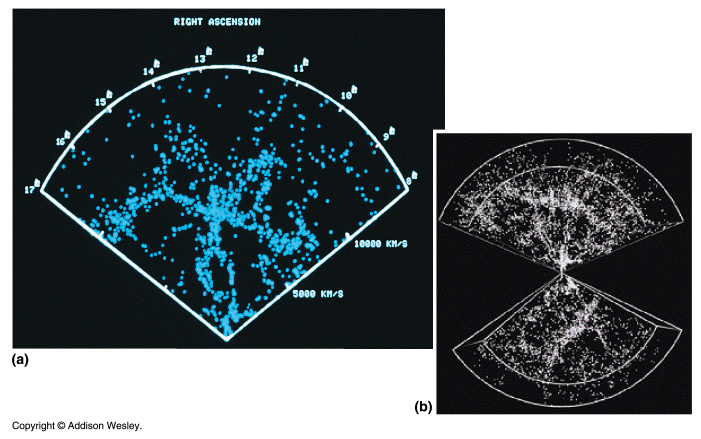By Measuring the redshifts of galaxies and using the Hubble Law to determine their distances we can map out the Large Scale Structure of the Universe.
Galaxies and clusters define "bubbles" of size ~ 30 Mpc (100 million light years). Great voids with few galaxies surounded by walls and filaments of superclusters. |
largest cluster structures (i.e. the super-clusters) cannot have changed much since the formation of the Universe, so the clustering tells us something about the formation of the Universe itself. These structures must have formed from regions of Dark Matter (since it is the major component of the mass) in the early Universe which were slightly more dense than average. The regions would have initially been expanding as the Universe was expanding but eventually reached a point where their gravity pulled them together.
Computer simulations model how this process happened and gives rise to the structures we see today. |
We know that d = vt. And v = Hod. Therefore, the age of the Universe is to = 1/Ho.
If Ho = 50 km/s/Mpc then,
= 6.17x1017 s ·(1 yr/3.16x107) = 1.96x1010 yrs = 19.6 billion years.
If Ho = 80 km/s/Mpc then,
= 3.86x1017 s ·(1 yr/3.16x107) = 1.22x1010 yrs = 12.2 billion years.
(if we ignore the effects of a possible Cosmological Constant). Then we must conclude that the expansion was faster in the past: gravity is slowing it down. So the Universe must be in fact younger than the Hubble Time.
Globular stars clusters are thought to be between 11-15 billion years old: Possibly inconsistent with the expansion age. The discrepancy was worse in the past, but new data is causing us to date the globular clusters a bit younger and find the Universe a bit older. So things are starting to work out.
The Cosmological Principle states that on the largest scales the Universe must look the same for any observer in space. The Universe must therefore be Homogeneous (same average density) and Isotropic (looks the same in all directions).
Evidence to support these assumptions: (1) Largest structures are superclusters. Beyond that things seem to smooth out. (2) Cosmic Microwave Background Radiation the same everywhere.
NOTE: density can change with time. These assumptions are for all space at any given time.
The results are that there are 3 types of possible homogeneous and isotropic Universes and the global geometry of the Universe can be 1 of 3 possible geometries:
There is a critical average density (matter + energy) that makes the Universe globally flat. It is calculated from Einstein's equations:
crit = 3H2/8G If we choose Ho = 65 km/s/Mpc, then the current critical density is
crit,o = 8 x 10-30 g/cm3
> crit 
Positive Curvature: Closed. Volume is finite but unbounded.
= crit Zero Curvature: Flat. Volume is infinite.
< crit Negative Curvature: Open. Volume is infinite.
If < crit Universe Expands Forever.If = crit Universe Expands Forever, but stops at time equal to infinity.If > crit Universe Eventually Stops Expanding and Collapses Back to a Hot, Dense State. (Big Crunch). |
If the Universe Expands Forever:
If the Universe Stops Expanding and Collapses:
The Cosmological Constant:
When Einstein first worked out his solutions to the equations of general relativity for the Universe as a whole, he realized that it was unstable to gravity and would collapse under its own weight.
The completely general mathematical solution to the equations includes an arbitrary constant (
). Einstein recognized that the constant would act as a kind of pressure in the Universe (an anti-gravity if you will) that acts over large distances (it grows stronger with greater distance!).
So he included it and gave it just the right value to keep the Universe static. Then it was discovered that the Universe was expanding and he no longer needed to consider the Cosmological Constant. He called it his "greatest blunder".
For most of the 20th Century people generally regarded the Cosmological Constant to be unphysical and therefore set its value to zero.
Recently, the study of white dwarf supernovae in distant galaxies has shown that they are too far away for their redshift (exactly the opposite of what was expected). Thus the Universe has not been decelerating but rather accelerating! This is the effect that we would expect from a non zero Cosmological Constant.
The results are still controversial. STAY TUNED!
If there is a non-zero Cosmological Constant it would contribute an energy density to the Universe and thus help shape the global geometry.
However, the fate of the Universe would now be disconnected from the geometry. As the matter density drops the Cosmological Constant would grow stronger causing the Universe to expand faster and faster. Thus it is possible for any geometry (Open, Flat, or Closed) to expand forever and an ever increasing rate.
NOTE: if the Universe is accelerating then the age of the Universe could be older than the Hubble Time since the Universe would have been expanding slower in the past.
Return to Class Notes Page
