Astronomy 10: Lecture 11
Lecture 11
Monday, June 17th 2002. Reading: Cosmic Perspective Chapters S2 & S4
Quiz
- Is there Gravity in space? What keeps Earth in orbit around the Sun?
- Where is the Moon in its orbit about the Earth during a Solar Eclipse? What Phase is that position Always?
- Where is the Moon in its orbit about the Earth when it is a crescent? Can it ever been seen overhead by anyone on Earth when it is midnight?
- You have three friends who all have babies born on the same day. One lives in Sacramento, Another in Chicago, and the other in New York City. They each send you a picture of their baby via US Postal Ground Service (i.e. all shipped via trucks). They each take the picture immediately before sending it to you. Mail from New York takes 5 days to reach Berkeley, Mail from Chicago takes 3 days, and mail from Sacramento takes 1 day. You receive all three pictures on the same day. Which baby appears to be the youngest in the picture?
Special Relativity
Einstein's theory of Relativity came in two parts. The first was published in 1905 and dealt only with objects that are moving with respect to each other at constant velocities. Thus each object has an indistinguishable reference frame from the other.
The theory is built on 2 basic assumptions:
Postulate #1: The Laws of Nature are the same for everyone
- When you are on an airplane, train, bus, or whatever and you have the window shades down and the ride is smooth you do not notice that you are moving with respect to the Earth.
- If you do physics experiments to test the laws of nature you will find the same form for these laws as anyone at rest with respect to the Earth would find.
There is, in fact, no absolute standard of rest. -- Recall Spaceship Earth.
Our point of view will be relative and so we seek to understand how we can view events from one frame while in another.
Relative Velocity
Einstein asked, "What would the world look like if one could travel on a beam of light?"
We must first be sure to understand what the world looks like at slower speeds. So let us do some thought experiments.
Let's just focus on the relative motion of a pair of friends: You and Jackie.
-Both are far from Earth's (or any other planet's) gravity for simplicity.
-Each has a small space craft which has big windows on the side that allow them to see inside each others craft.
Let's say that You are moving to the right past Jackie with some constant velocity, v.
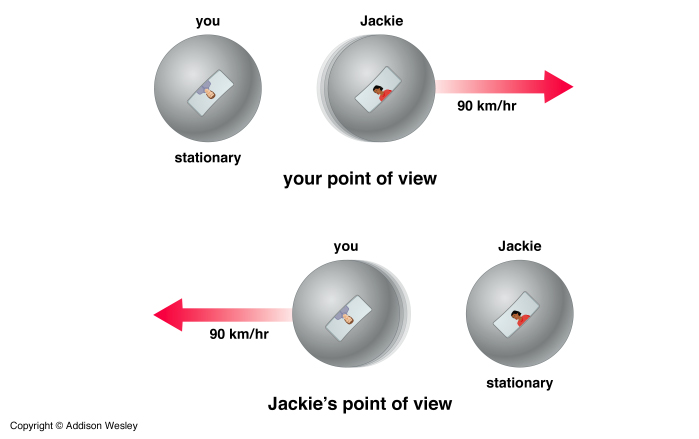 You could claim that you are not the one moving, but rather it is Jackie who is moving to the left past you with the same constant velocity, v. Who is right?
You could claim that you are not the one moving, but rather it is Jackie who is moving to the left past you with the same constant velocity, v. Who is right?
Both are! Each frame is equally valid. Since there are no accelerations on either frame there is no way to distinguish one from the other.
|
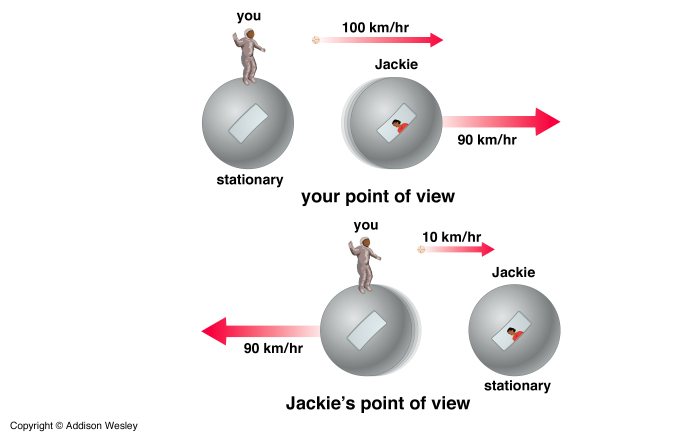 As Jackie watches You go by she sees you throw a ball toward the Right from your craft. You throw the ball with velocity, u, with respect to your craft. What is the speed of the ball as seen by Jackie?
As Jackie watches You go by she sees you throw a ball toward the Right from your craft. You throw the ball with velocity, u, with respect to your craft. What is the speed of the ball as seen by Jackie?
Common sense tells us that we should simply add the speed of the ball to the speed of the craft. v' = u + v
|
The Speed of Light
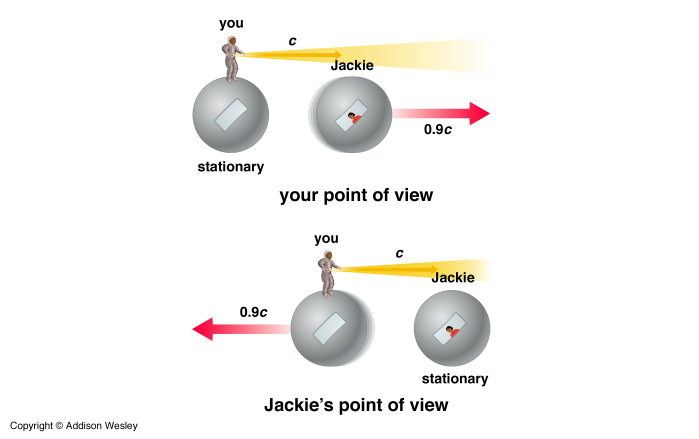 Now, You pull out a flashlight and send a beam of light toward the front of your spacecraft. What is the velocity of the light as observed by Jackie?
Now, You pull out a flashlight and send a beam of light toward the front of your spacecraft. What is the velocity of the light as observed by Jackie?
Should it not simply be: c' = c + v ?
|
No!
If the speed of light were able to simply add we would have a paradox in many experiences.
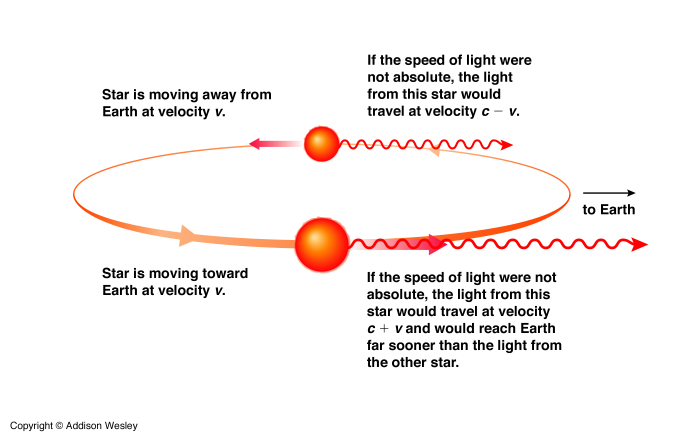 Example 1: Consider a star in a binary system. Sometimes it is moving toward Earth with its orbital speed, v, and other time it is moving away. When it comes toward you the speed of the light coming toward you will be faster than the light that you see when the star is moving away.
Example 1: Consider a star in a binary system. Sometimes it is moving toward Earth with its orbital speed, v, and other time it is moving away. When it comes toward you the speed of the light coming toward you will be faster than the light that you see when the star is moving away.
At a great enough distance or great enough orbital speed you could see the light from the star moving toward you arrive at the same time as the light from the star moving away from you, on the other side of the orbit. You could see the star appear in multiple positions at once! This is never observed.
|
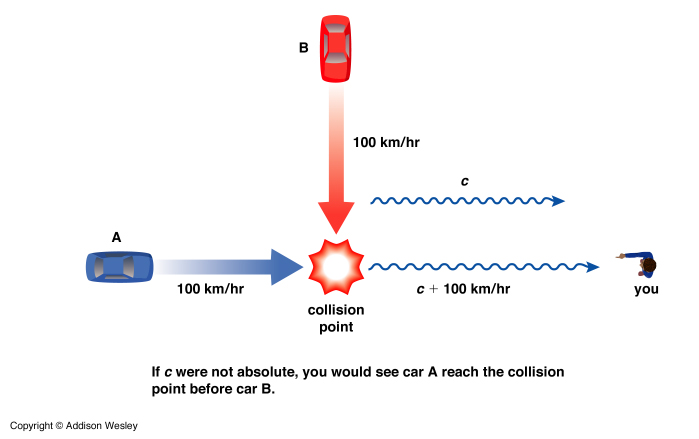 Example 2: Consider two cars, A and B, headed toward an intersection. Both cars are equally far from the intersection and are headed toward it at 100 km/hr. They will collide when they reach the intersection. However, if you are standing straight down the street in the direction that car A is heading you will see the light from car A moving faster than the light from car B. Thus, you would see car A get to the intersection before car B and thus there should be no collision.
Example 2: Consider two cars, A and B, headed toward an intersection. Both cars are equally far from the intersection and are headed toward it at 100 km/hr. They will collide when they reach the intersection. However, if you are standing straight down the street in the direction that car A is heading you will see the light from car A moving faster than the light from car B. Thus, you would see car A get to the intersection before car B and thus there should be no collision.
What!? That's not possible. The collision happens, it should not depend on where we are located as to whether or not we see the collision to occur.
|
These two illustrations say that something is wrong with our assumption that we can just add the velocity of light to the motion of whatever emitted it.
In fact they say that in order for things to make sense the speed of light should be the same for everyone no matter what speed they have relative to it.
Indeed, electromagnetic theory at the end of the 19th century was saying the exact same thing, only no had yet realized it. The speed of light is a constant for all observers. That is the second assumption of special relativity.
Postulate #2: The speed of light (in a vacuum) is the same for everyone
This has been experimentally verified again and again for the past 90-some-odd years. No matter who emits the light and at what relative velocity, everyone measures it to have the same speed, c = 3 x 108 m/s.
Thus when You shine your flashlight you measure the speed to be, c, and when Jackie observes the light of your flashlight she also measures the speed of the light to be c, not c + v!
Universal Speed Limit
The fact that light must be measured the same by all observers requires that no material object can exceed, or even attain, the speed of light.
Consider that Jackie now goes speeding off in her spacecraft. She throws the craft into high gear, firing the rockets to incredible speed. Now she turns on her head lights.
In her frame the lights go zooming out ahead of her at the speed of light (no faster, no slower). In her own frame it is impossible for her to overtake her headlights since the speed of light must always be constant.
Can anyone else observe her to move faster than light?
People in different frames will measure her to have different speeds relative to themselves, but they will all agree on two things.
- The light of her headlights is moving out in front of her
- it has the speed, c.
Clearly, if she is being outraced by her headlights and her headlights are traveling at the speed of light, she must be traveling slower than the speed of light.
This is not merely some technological challenge. No material object may even reach the speed of light. This is the law of nature. There are no penalties for violating the law, because it cannot be broken.
Simultaneity
Another fact that results from the constancy of the speed of light is that no two relative observers can agree on the simultaneity of events.
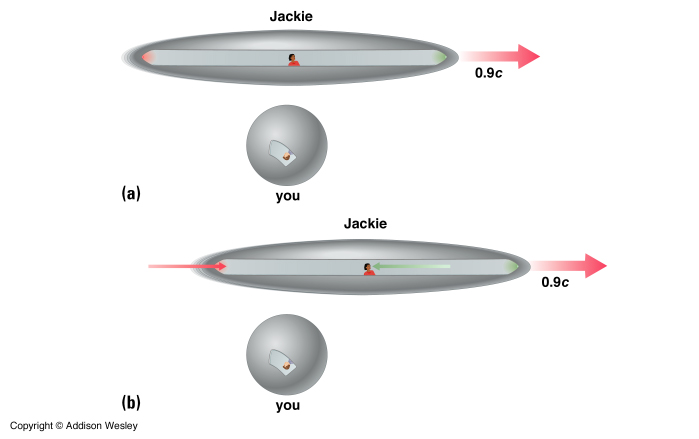 Consider Jackie racing by You in her spaceship. She has a green light in the front of her craft and a red light in the rear. At the moment that Jackie and You are lined up (the shortest distance between each other) the two lights flash in Jackie's ship. Since You are equal distances from the lights You will see the light reach You at the same time, and conclude that the flashed were simultaneous. You will see Jackie lit up first by the green and then by the red since she is moving toward the red.
Consider Jackie racing by You in her spaceship. She has a green light in the front of her craft and a red light in the rear. At the moment that Jackie and You are lined up (the shortest distance between each other) the two lights flash in Jackie's ship. Since You are equal distances from the lights You will see the light reach You at the same time, and conclude that the flashed were simultaneous. You will see Jackie lit up first by the green and then by the red since she is moving toward the red.
From Jackie's point of view she is racing toward the green light and intercepts that light first and then the red light catches up to her. Since the lights are also equal distances from her she must conclude that the green light flashed before the red light did. Curiouser and Curiouser.
|
They agree on the outcome, but not the timing of the events separated by a distance.
Note: All observers must observed the same order of events that occur at the same location. For example if you pick up and eat a cookie, no one will see you to eat the cookie first and then pick it up.
Velocity Addition
Now that we see that it is indeed impossible to travel at speeds greater than the speed of light, we wonder what about the addition of velocities.
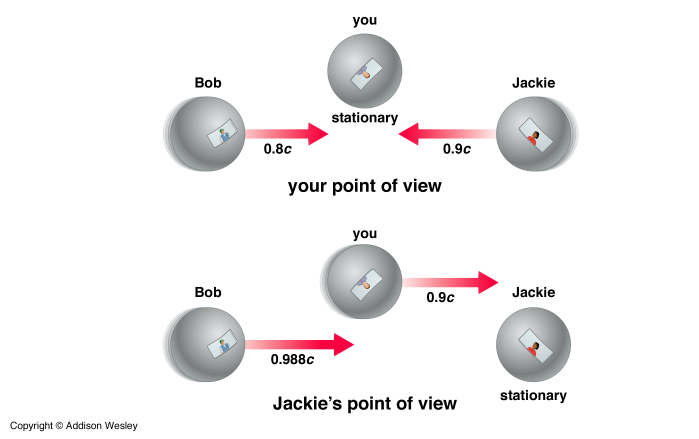 Imagine that a fellow Bob is heading toward Jackie at 80% the speed of light from your frame of reference. Jackie is heading toward Bob at 90% the speed of light as seen by You. How fast does Jackie see You and Bob coming at her?
Imagine that a fellow Bob is heading toward Jackie at 80% the speed of light from your frame of reference. Jackie is heading toward Bob at 90% the speed of light as seen by You. How fast does Jackie see You and Bob coming at her?
By just adding velocities you would get 170% the speed of light for Bob. That is clearly not right. She must see Bob moving slower than the speed of light but also faster than 90% the speed of light. As it turns out she will see it coming at her at 98.8% the speed of light.
|
Time Dilation
Consider a thought experiment. Imagine that Bob is in a train moving to the right with some speed, v, relative to the ground on which Jackie is standing watching him go by.
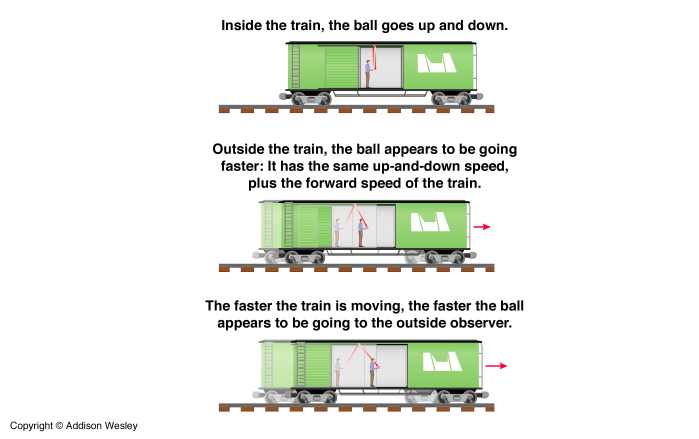 Bob has a ball that he is casually tossing up and catching as it falls back down. From Bob's perspective the ball goes straight up and straight down and therefore has no forward motion.
Bob has a ball that he is casually tossing up and catching as it falls back down. From Bob's perspective the ball goes straight up and straight down and therefore has no forward motion.
But Jackie sees the ball take a different path. From her perspective the ball has a forward velocity given it by the train so that the ball appears to take a slanted path. It leaves Bob's hand and slants forward and then falls back to Bob's hand, which has moved in the time interval because of the motion of the train. The ball therefore takes a longer path than the one that Bob sees. That's fine because the ball travels faster as seen by Jackie than Bob. So there's no paradox. As the train's speed increases the slant grows larger and thus the ball takes a longer path and thus must be traveling faster.
|
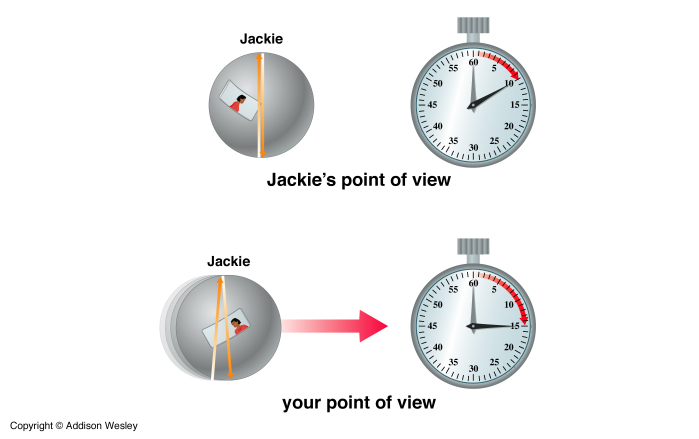
Now imagine a similar situation. This time Jackie has a clock that works by measuring the time difference between a beam of light emitted from the bottom of the clock which reflects off a mirror on the top of the clock and then is detected back on the bottom of the clock: one tick of the light clock.
Now Jackie gets in her spacecraft with the light clock and goes speeding off. You observe her passing by and watch the light clock. The light in the clock will now take a path just like that of the ball in the previous thought experiment, a slanted path. The difference in this case is that the speed of the light as seen by You is the same as that seen by Jackie. But You see the light take a longer path than Jackie sees it to take. Therefore You think the light takes a longer time to make one tick. But to Jackie in the spacecraft the light clock is running just like it did before she got in the spacecraft.
You therefore must conclude that Jackie's time is running slower than yours. The faster Jackie's speed relative to You the longer the light's path and thus the longer it will take to complete one tick. So as the speed increases Jackies's clock seems to run slower and slower.
It's not just the light clock, it's time itself that is running slower in Jackie's spaceship.
What does Jackie see? To make this easier to understand, imgagine that You are in another spacecraft as we earlier considered, and they have a relative speed between them of, v. Now, it doesn't matter who is moving. You think You are stationary and Jackie is moving away at v, likewise Jackie thinks that she is stationary and it is You that is moving away from her. Both viewpoints are valid. You have a light-clock just like hers. Therefore she will see YOUR time to run slower than hers. Wow, that's weird!
|
This effect is called time dilation. From your point of view time runs slower for anyone moving relative to you. As the their speed approaches the speed of light time seems to stop.
This effect has been experimentally verified. Very accurate atomic clocks have been taken aboard jet airplanes that flew in circles for hours. When the clocks aboard the plane were compared to clocks on the ground they had lost a few nanoseconds of time. Exactly the amount predicted by special relativity. The effect is obviously inperceptible at normal speeds. But as speeds approach the speed of light it is much more noticeable.
In particle accelerators, physicists accelerate particles to near the speed of light and smash them into each other. In the collisions new particles are formed. One such particle is the muon. When at rest this particle lives only 2.2 microseconds before decaying into other particles. But in experiments where it is created moving at 99% the speed of light it last for 15.6 microseconds, which is exactly the amount predicted by special relativity.
Length Contraction
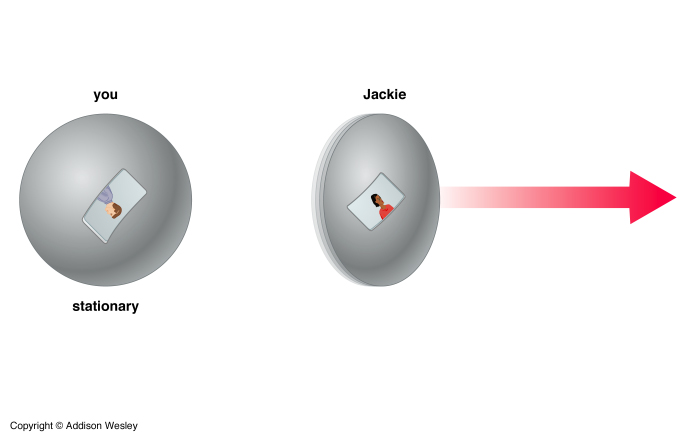 Now, imagine that Jackie goes zipping by Your spaceship. She makes a measurement of your spaceship's length. She does this by timing how long it takes for her to cover the distance between the front end and back end of your ship moving at the relative speed between them. Because You see her time running slower than your own she will seem to pass over your length in less time than you would expect. Thus she measures your ship's length to be shorter than what it is at rest. Likewise You measures her ship to be shorter than what she thinks it is.
Now, imagine that Jackie goes zipping by Your spaceship. She makes a measurement of your spaceship's length. She does this by timing how long it takes for her to cover the distance between the front end and back end of your ship moving at the relative speed between them. Because You see her time running slower than your own she will seem to pass over your length in less time than you would expect. Thus she measures your ship's length to be shorter than what it is at rest. Likewise You measures her ship to be shorter than what she thinks it is.
This effect is called length contraction. It occurs only along the direction of motion. From your point of view, lengths of objects moving by you (or distances between objects moving by you) are shorter in their direction of motion than they would be if they were at rest with respect to you. The faster the objects are moving, the shorter the lengths. As they approach the speed of light their lengths contract to zero.
|
|
Think about the Muon in the above experiment. When created it should only make it a fraction of the way through the particle accelerator before decaying. But instead it makes it all the way through. Why? In its reference frame the length of the accelerator has shortened. It has less of a distance to travel. What we interpret as a time dilation for it, it sees as a length contraction.
|
|
Time and Space are intimately related to one another.
|
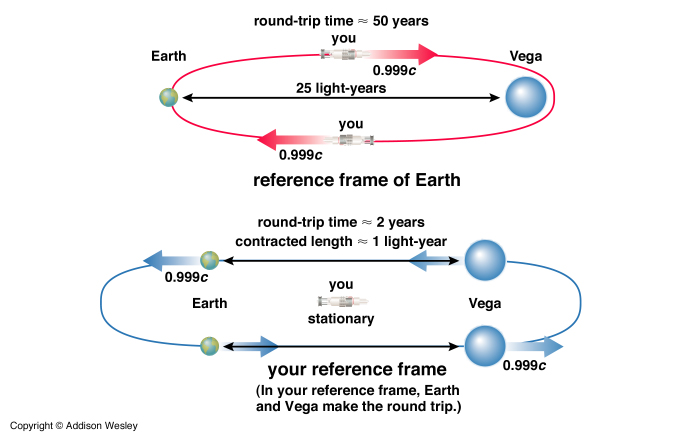
This effect allows us to reach the stars in a reasonable amount time. Consider a trip to the star Vega, which lies at a distance of 25 light-years. At conventional speeds it would take eaons to reach Vega. But imagine that Jackie goes off to Vega in her spacecraft at 99.9% the speed of light. Because Jackie can view herself as stationary and Vega is rushing at her at 99.9% the speed of light the distance will contract to just over 1 light-year. So she will make it there in just a little longer than a year. She can then return and the total round trip time for her is only about 2 years. However, on Earth You saw her take off at near the speed of light and so if it takes light 25 years to make it to Vega and another 25 to make it back, 50 years will have passed on Earth. You are now 48 years older than Jackie.
One could make even longer journies. Imagine that Jackie heads off to the nearest spiral galaxy, Andromeda (M31) at 2.5 million years distance. At sufficient speed she could make it there in 25 years. The round trip is then only 50 years. If she left when she was 20 she'd return when she was 70. However, on Earth 5 million years would have passed.
|
This is a form of Time Travel into the future. But there's no return trip (or is there? ... Bum Ba Baah)
Mass Increase
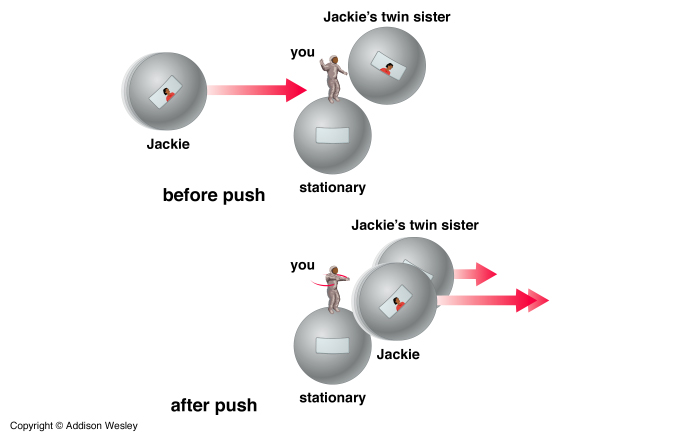 Imagine that Jackie is in her spacecraft and You are floating out in space right next to the craft ready to give it a push. Bob's ship comes doodiddlin' along at a relative speed, v. Now both Jackie and Bob are identical in mass and so are their ships (at rest anyway). You give them both an identical push at the moment that Bob passes you. That means you applied an identical force. But, Bob's clock is running slow as seen by you and Jackie. Hence your push on Bob's ship happens over a shorter time than the push on Jackie's ship. Therefore your equal pushes produce different accelerations on Jackie and Bob's ships. Bob's ship accelerates less because it felt the force for a shorter time. The only way this can be is if you measure Bob's mass to be greater than Jackie's.
Imagine that Jackie is in her spacecraft and You are floating out in space right next to the craft ready to give it a push. Bob's ship comes doodiddlin' along at a relative speed, v. Now both Jackie and Bob are identical in mass and so are their ships (at rest anyway). You give them both an identical push at the moment that Bob passes you. That means you applied an identical force. But, Bob's clock is running slow as seen by you and Jackie. Hence your push on Bob's ship happens over a shorter time than the push on Jackie's ship. Therefore your equal pushes produce different accelerations on Jackie and Bob's ships. Bob's ship accelerates less because it felt the force for a shorter time. The only way this can be is if you measure Bob's mass to be greater than Jackie's.
F = ma
From your point of view, objects moving past you have a greater mass than they have at rest. The faster an object is moving the greater the increase in mass. As you increase the speed toward the speed of light the mass becomes infinte. Thus it would take infinte force or infinite energy to accelerate any mass to the speed of light. This is why it was stated earlier that no material object may move at the speed of light.
|
Mass-Energy Equivalence
Einstein's famous equation relating Mass and Energy is actually a direct result of the effects of special relativity discussed above.
E = mc2
This equation is derived mathematically by taking the equation for mass increase and rewritting it. You eventually end up with terms that look like Kinetic energy and an extra term, one for what we call rest mass: the energy associated with an object at rest. Another way we may derive the equation is to try and figure out what the kinetic energy is of a moving mass and use the mass increase formula.
The equation says that just as Space and Time are not the separate things they appear to be Mass and Energy are also two sides of the same coin. When we look at it in one way we see Mass when we look at it another we see Energy. Likewise when we look at it in one way we see Space, when we look at it another way we see Time. This lead to the concept of the Spacetime Continuum.
Quantum Mechanics
The Standard Model
Matter and Energy are broken into fundamental (quantum) units which we generally call particles.
The Standard Model of quantum mechanics classifies particles based on their basic properties: Mass, Charge, and Spin. Spin is related to the angular momentum of a particle. The first classification is based on Spin. Particles fall into two classes:
- Bosons - have integer Spin (0, 1, 2, etc.), example: Photons.
- Fermions - have half-integer spin (1/2, 3/2, 5/2, etc), examples: electrons, neutrons, and protons.
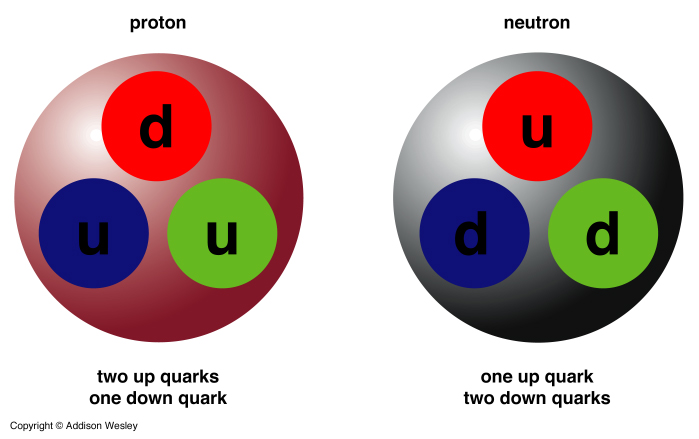
As previously mentioned Protons and Neutrons are not fundamental particles as they are made of smaller particles calld Quarks. Electrons do seem to be fundamental. The fundamental Fermions are sub-classified as either Leptons or Quarks. There are six kinds of each predicted by the Standard Model.

The Top Quark was predicted to exist but not observed until quite recently (1995).
Antimatter
The Standard Model actually predicts 12 fundamental Fermions. Each particle has an antiparticle. An antiparticle has all the same properties of its counterpart but with the opposite charge. So the anti-electron (also known as a positron) has the same mass and spin as an electron but has a positive charge instead of a negative charge.
When a particle and its antiparticle meet they mutually annihilate one another and convert all their mass into energy producing a photon having the exact energy of the combined particles (via E = mc2). The process can actually happen in reverse. A high energy photon can turn into a particle-antiparticle pair. The antiparticle will generally soon find a particle to annihilate with again to create another photon of the same energy. This is called pair production.
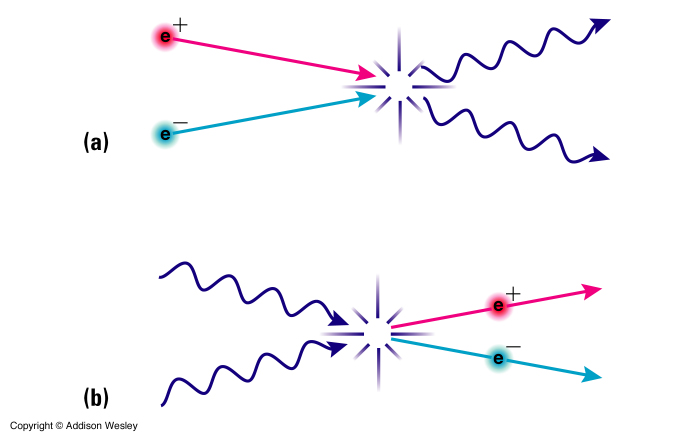
The fact that matter exist at all in the Universe means that there is very little antimatter present in the Universe. Else there would be constant annihilation and the Universe would be full of gamma-rays.
 You could claim that you are not the one moving, but rather it is Jackie who is moving to the left past you with the same constant velocity, v. Who is right?
You could claim that you are not the one moving, but rather it is Jackie who is moving to the left past you with the same constant velocity, v. Who is right?
 As Jackie watches You go by she sees you throw a ball toward the Right from your craft. You throw the ball with velocity, u, with respect to your craft. What is the speed of the ball as seen by Jackie?
As Jackie watches You go by she sees you throw a ball toward the Right from your craft. You throw the ball with velocity, u, with respect to your craft. What is the speed of the ball as seen by Jackie?
 Now, You pull out a flashlight and send a beam of light toward the front of your spacecraft. What is the velocity of the light as observed by Jackie?
Now, You pull out a flashlight and send a beam of light toward the front of your spacecraft. What is the velocity of the light as observed by Jackie? Example 1: Consider a star in a binary system. Sometimes it is moving toward Earth with its orbital speed, v, and other time it is moving away. When it comes toward you the speed of the light coming toward you will be faster than the light that you see when the star is moving away.
Example 1: Consider a star in a binary system. Sometimes it is moving toward Earth with its orbital speed, v, and other time it is moving away. When it comes toward you the speed of the light coming toward you will be faster than the light that you see when the star is moving away. Example 2: Consider two cars, A and B, headed toward an intersection. Both cars are equally far from the intersection and are headed toward it at 100 km/hr. They will collide when they reach the intersection. However, if you are standing straight down the street in the direction that car A is heading you will see the light from car A moving faster than the light from car B. Thus, you would see car A get to the intersection before car B and thus there should be no collision.
Example 2: Consider two cars, A and B, headed toward an intersection. Both cars are equally far from the intersection and are headed toward it at 100 km/hr. They will collide when they reach the intersection. However, if you are standing straight down the street in the direction that car A is heading you will see the light from car A moving faster than the light from car B. Thus, you would see car A get to the intersection before car B and thus there should be no collision.
 Consider Jackie racing by You in her spaceship. She has a green light in the front of her craft and a red light in the rear. At the moment that Jackie and You are lined up (the shortest distance between each other) the two lights flash in Jackie's ship. Since You are equal distances from the lights You will see the light reach You at the same time, and conclude that the flashed were simultaneous. You will see Jackie lit up first by the green and then by the red since she is moving toward the red.
Consider Jackie racing by You in her spaceship. She has a green light in the front of her craft and a red light in the rear. At the moment that Jackie and You are lined up (the shortest distance between each other) the two lights flash in Jackie's ship. Since You are equal distances from the lights You will see the light reach You at the same time, and conclude that the flashed were simultaneous. You will see Jackie lit up first by the green and then by the red since she is moving toward the red.
 Imagine that a fellow Bob is heading toward Jackie at 80% the speed of light from your frame of reference. Jackie is heading toward Bob at 90% the speed of light as seen by You. How fast does Jackie see You and Bob coming at her?
Imagine that a fellow Bob is heading toward Jackie at 80% the speed of light from your frame of reference. Jackie is heading toward Bob at 90% the speed of light as seen by You. How fast does Jackie see You and Bob coming at her?
 Bob has a ball that he is casually tossing up and catching as it falls back down. From Bob's perspective the ball goes straight up and straight down and therefore has no forward motion.
Bob has a ball that he is casually tossing up and catching as it falls back down. From Bob's perspective the ball goes straight up and straight down and therefore has no forward motion.

 Now, imagine that Jackie goes zipping by Your spaceship. She makes a measurement of your spaceship's length. She does this by timing how long it takes for her to cover the distance between the front end and back end of your ship moving at the relative speed between them. Because You see her time running slower than your own she will seem to pass over your length in less time than you would expect. Thus she measures your ship's length to be shorter than what it is at rest. Likewise You measures her ship to be shorter than what she thinks it is.
Now, imagine that Jackie goes zipping by Your spaceship. She makes a measurement of your spaceship's length. She does this by timing how long it takes for her to cover the distance between the front end and back end of your ship moving at the relative speed between them. Because You see her time running slower than your own she will seem to pass over your length in less time than you would expect. Thus she measures your ship's length to be shorter than what it is at rest. Likewise You measures her ship to be shorter than what she thinks it is.

 Imagine that Jackie is in her spacecraft and You are floating out in space right next to the craft ready to give it a push. Bob's ship comes doodiddlin' along at a relative speed, v. Now both Jackie and Bob are identical in mass and so are their ships (at rest anyway). You give them both an identical push at the moment that Bob passes you. That means you applied an identical force. But, Bob's clock is running slow as seen by you and Jackie. Hence your push on Bob's ship happens over a shorter time than the push on Jackie's ship. Therefore your equal pushes produce different accelerations on Jackie and Bob's ships. Bob's ship accelerates less because it felt the force for a shorter time. The only way this can be is if you measure Bob's mass to be greater than Jackie's.
Imagine that Jackie is in her spacecraft and You are floating out in space right next to the craft ready to give it a push. Bob's ship comes doodiddlin' along at a relative speed, v. Now both Jackie and Bob are identical in mass and so are their ships (at rest anyway). You give them both an identical push at the moment that Bob passes you. That means you applied an identical force. But, Bob's clock is running slow as seen by you and Jackie. Hence your push on Bob's ship happens over a shorter time than the push on Jackie's ship. Therefore your equal pushes produce different accelerations on Jackie and Bob's ships. Bob's ship accelerates less because it felt the force for a shorter time. The only way this can be is if you measure Bob's mass to be greater than Jackie's.


