Math Review #1
This is a review of the mathematical concepts we have encountered in this course. It is not extensive. If you feel you need more basic review than this you should visit the following web site: Math for Morons Like Us (I didn't come up with the name)
Geometry
Right Triangles
You'll find that in this course whenever we need to make a measurement of distance that right triangles will be of use. A right triangle is one in which one of the angles is a 90° angle. Recall that the sum of the angles of any triangle is 180°. The relationships between the lengths of the sides of a right triangle and the angles in the triangle are very important. Consider the following figure
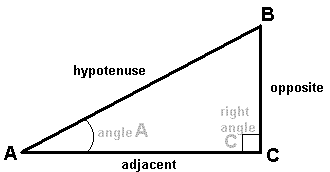
The first thing to remember is that the lengths of the sides of a right triangle are related by the Pythagorean theorem:
(hypotenuse)2 = (opposite)2 + (adjacent)2
This says that the sum of the squares of the "legs" of a triangle (the two sides that meet in the 90° angle) are equal to the square of the hypotenuse (the side that is opposite the 90° angle).
The next thing to remember is the trigonometric functions that relate the ratios of the lengths of the sides of the right triangle to its angles. For angle A in the figure the relations are:
COS(A) = adjacent/hypotenuse
SIN(A) = opposite/hypotenuse
TAN(A) = Cos(A)/SIN(A) = opposite/adjacent
Circles and Spheres
The other shapes that will come up again and again in astronomy are circles and spheres. A circle is the set of points that all lie a given radius, r, away from any specific point in 2-dimensions. A sphere is the same thing but in 3-dimensions.
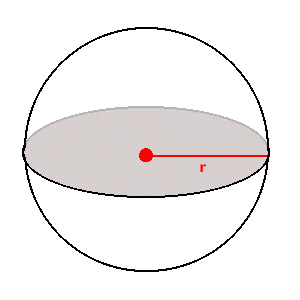
The length around a circle is called the circumference. The ratio of circumference, C, to the diameter, D (D = 2r), is the transcendental number represented by the Greek letter  . Hence,
. Hence,
C = 2 r
r
The ratio of the area, A, of a circle to the square of the radius is again  . Hence,
. Hence,
A =  r2
r2
For a sphere the 3-D equivalent of Circumference is Surface Area, SA. It is given by
SA = 4 r2
r2
Finally, the volume, V, of a sphere is given by
V = (4/3) r3
r3
Ellipses
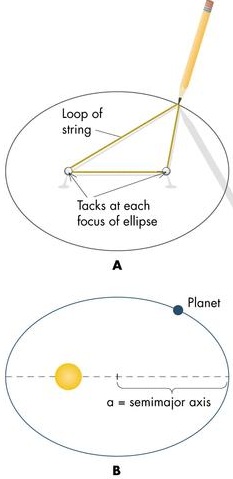 |
An ellipse is the set of points whose sum of distances to two fixed points (called foci, focus singular) is the same. One way to draw an ellipse is to attach the ends of a string to two fixed points and pull the string tight with a pencil and circle around the points. The long axis of the ellipse is called the major axis, the short axis is called the minor axis. The distance from the center out to the ellipse along the major axis is called the semimajor axis, usually denoted with the letter a. Circles are just special ellipses. They are ellipses with both foci at the same point. |
Measuring Angles
The ancient Babylonians devised the system of degrees where a circle is divided into 360 equal angles each one having one degree (1°) of arc. Each degree can further be divided into 60 arc minutes (1° = 60'), and each arc minute can be divided into 60 arc seconds (1' = 60"). There is another measure of angles which is a natural result of the connection of angles to circles. It is called the radian. Radians are a pure number and as such have no units. So if ever you see an equation with an angle equal to a unitless quantity it must be measured in radians. There are 2 radians in a circle. Therefore 360° = 2
radians in a circle. Therefore 360° = 2 radians, or 1 radian = 57.3°. In astronomy we typically use the arc second as a measure of angle in the sky. So it's useful to remember that there are 57.3° * 60'/1° * 60"/1' = 206,265" in 1 radian.
radians, or 1 radian = 57.3°. In astronomy we typically use the arc second as a measure of angle in the sky. So it's useful to remember that there are 57.3° * 60'/1° * 60"/1' = 206,265" in 1 radian.
Understanding of these simple geometric figures and relations allowed the ancient Greeks to make measurements of the size of the Earth, Moon, Sun and their distances from one another.
What's a Radian?
Measuring angles in Radians uses the connection between angles and circles to find a convenient and natural unit of measurement.
An angle, A, measured in radians is the ratio of the arc length, l, swept out at a radius, r, to the radius, r:
A = l/r
The arc length swept out by a full circle is l = 2 r, and so the number of radians in a circle is A = 2 r, and so the number of radians in a circle is A = 2 r/r = 2 r/r = 2 . Since radians are a ratio of two lengths they are clearly unitless. . Since radians are a ratio of two lengths they are clearly unitless.
|
 |
Small Angle Approximation
Consider a linear length, D, at a distance, d, from some given point, which subtends an angle, A. If the angle, A, is small, then D 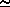 l, and d
l, and d  r. Therefore the angle, A, can be approximated as
A
r. Therefore the angle, A, can be approximated as
A  D/d.
D/d.
Angular Size
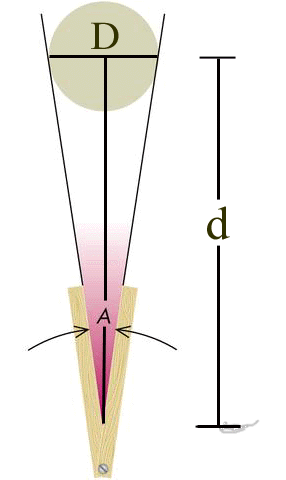 |
The Angular Size, A, and Physical Size, D, are related to one another through the distance, d, of an object and the Tangent function.
Tan(A/2) = (D/2)/d
Use the Small Angle Approximation:
Tan(A/2)  A/2 A/2
A 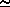 D/d D/d
|
Speed, Time, Distance, and Acceleration
Speed is the amount of distance covered per unit time by a moving object. Another way of saying this is that it's the amount of change in position per unit time. Velocity is the speed + direction of an object. It is what we call a vector quantity. Speed has units of distance/time (i.e., m/s). The relationship between distance, speed, and time is simply
d = vt
Where d, is the distance covered, and t is the time in which it was covered while traveling at a constant speed, v.
Acceleration is the amount of change in velocity per unit time. It has units of distance/time/time (i.e., m/s2). The distance that an object moves in a span of time, t, with a constant acceleration, a, and an initial velocity, v0, is given by
d = v0t + (1/2)at2
Return to Class Notes Page


![]() . Hence,
. Hence,
![]() . Hence,
. Hence,

