Homework #5 Solutions

Homework #5 Solutions

  1. Sunsets are Red, the Sky is Blue...

    "White light," emitted by the Sun, and other G-type stars, is a mixture of all colors with equal intensities.
    1. When you look up into the sky, why does the part away from the Sun look blue?

      During the day, when you look up into the sky, you usually see the color blue (unless of course you are looking right at the Sun or if it's a really cloudy day). The reason for the blue color is that you are seeing light that is scattered by molecules in the atmosphere into your line of sight --- your eyes, that is. Blue light is more likely to scatter than red light, so we see the sky as blue.

    2. Why does the Sun look red at sunset? What happens to the blue light?

      At sunset the sun's rays are shining through a thick portion of the atmosphere. We mentioned in part (a) that blue light is preferentially scattered. Thus light that is shining through a thick portion of the atmosphere will appear red since bluer light has already been scattered out. Absorption by dust also removes some of the blue light.

    3. In what ways are your above answers analogous to the explanations for the bluish color of reflection nebulae and the process of interstellar reddening?

      Similarly, reflection nebulae appear bluish since they preferentially scatter blue light. The process of interstellar reddening, whereby stars appear redder than they really are, is explained by the fact that the bluer light from the stars is preferentially scattered and absorbed out. (Note that this has nothing to do with the redshift, which is due to motion.)

  2. There's More Than Nougat in the Milky Way

    1. Draw a edge-on-view diagram of our Galaxy. Label all of the following: disk, halo, bulge, globular clusters, open clusters, and the location of the Sun. (2 points)

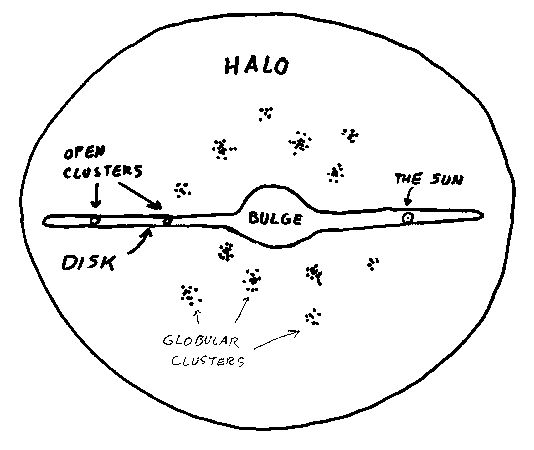
    2. How do we know the location of the Sun within our Galaxy? (2 points)

      Harlow Shapley noticed that most of the globular clusters in the Milky Way were concentrated in one general direction. He developed a technique to measure the distances to globular clusters and when he did so, found that the globular clusters are centered not around the Sun, but around a point 8 kpc from the Sun. He deduced that this point must be the center of the Galaxy, because the orbits of the globular clusters would necessarily be around the center of the galaxy.

  3. Stellar Populations and Spiral Structure

    1. In terms of stellar populations, why do spiral arms tend to be bluer than the rest of the Galaxy?

      Most of our Galaxy's star formation takes place in spiral arms. The blue color of the spiral arms is due to the the O and B type stars that were formed within them. Since O and B type stars are short lived, they do not exist long enough to leave the spiral arms. Only much less massive, and more red, stars, live long enough to leave the spiral arm where they formed. Thus the spiral arms are more blue than the the nonspiral portions of the disk of our Galaxy.

    2. If a type II supernova were to occur in our Galaxy, would you expect it to occur within a spiral arm, or outside of a spiral arm? Why?

      You would expect that it would be in a spiral arm. Only very massive stars undergo type II supernovae. Very massive stars are short lived. Since, they will live out their entire life very quickly, they do not have time to leave the spiral arm where they formed.

    3. Why do we not believe that the spiral arms are material spiral arms?

      Let's assume that the arms ARE made up of material. That material would then be subject to differential rotation. Differential rotation means that objects closer to the center of the galaxy rotate about the center of the galaxy more quickly than objects farther out. This would then cause the material to twist into a spiral. Here is the problem: Compare the age of our galaxy (about 1010years) and the time it would take for a star, say, at the Sun's distance from the galactic center to complete an orbit (about 2x108 years). There have been about 50 orbits of the galaxy at this distance! This kind of number means that if differential rotation caused material spiral arms, then those spiral arms would be VERY tightly wound. We do not observe spirals this tight neither in our own galaxy, nor others.

    4. What do we believe is the cause of spiral structure in our Galaxy?

      We believe that the spiral structure of our Galaxy stems from spiral shaped density waves rotating through our galaxy. The density wave acts like a compression wave, bringing the stars closer together, and inducing star formation by inducing the formation of molecular clouds from atomic gas.

  4. Beware of the Dark Side

    The expression for the mass of the Milky Way Galaxy within a distance, r, from the center is M = v2r/G, where G is Newton's gravitational constant (numerically equal to 4.30 x 10-6(kpc/M)·(km/s)2) and v is the orbital speed of a star at distance r. This formula works equally well for other spiral galaxies. Thus, the mass of a galaxy as a function of radial distance from the center can be obtained from the rotation curve of the galaxy.

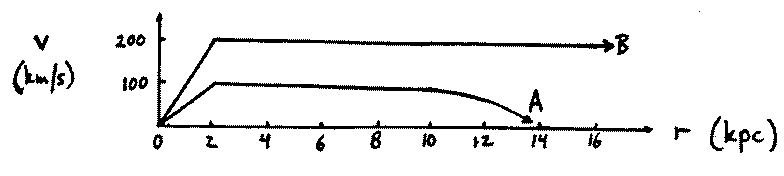
    1. Shown above are two possible rotation curves of the Milky Way Galaxy. (Niether one is necessarily correct.) If rotation curve B is correct, what is the mass of the Milky Way Galaxy within a radius of 10kpc? (Keep careful track of units, and express your answer in solar masses.)

      M = v2r/G

      If rotation curve B is correct, at r=10 kpc, v=200 km/s.

      Thus,

      M = (200 km/s)2 x (10 kpc) / (4.30 x 10-6(kpc/M)·(km/s)2)

      M = 9.3 x 1010M

    2. Compared with rotation curve B, does rotation curve A yield a larger, or smaller, mass for the Milky Way Galaxy within a radius of 8kpc? By What factor?

      According to the graph, rotation curve A indicates a velocity half that indicated by rotation curve B at r = 8 kpc. Since mass is proportional to velocity squared, the mass interior to a radius of 8 kpc indicated by curve A is 4 times as small (or 1/4 as large) as the mass indicated by curve B.

    3. Suppose rotation curve B is correct. If the luminous material (stars, gas) in the Milky Way Galaxy extends out to a radius of 14Kpc, and becomes quite faint beyond that, what must be true at radii larger than 14kpc?

      There must, then, be matter which is not luminous, which lies beyond 14 kpc.

  5. It May Be A Small World, But It's A Big Universe

    It is now known that our Galaxy is one of billions in a truly gargantuan Universe. But this was only discovered in the 1920s.
    1. Why did Harlow Shapley think that the "spiral nebulae" were contained within the Milky Way Galaxy, and that the Milky Way Galaxy was the entire extent of the Universe?

      1. Shapley's estimate for the size of the Milky Way Galaxy was much larger than had been previously thought and he reasoned that it was then large enough to contain the spiral nebulae.
      2. Recent data had showed them to be observed spinning, indicating that they must be close by if we can see it.
      3. The fact that the galaxies were not seen in the "zone of avoidance" indicated to him a galactic association for them.
      4. A nova was observed within the Great Nebula in Andromeda. To be visible it had to be close by (they didn't know about supernovas then).

    2. Why did Heber Curtis think that the "spiral nebulae" were actually "island universes"?

      1. Curtis's estimate was small for the size of the Milky Way Galaxy. If the spiral nebulae were all about the same physical size the varying angular sizes of the spiral nebulae would necessarily make them outside the Milky Way Galaxy.
      2. Curtis noticed the dark lanes in the spiral nebula and interpreted them as regions of obscuring dust. He reasoned that such obscuring dust in our own Galaxy would block out the light of objects beyond the disk of the Galaxy. Thus the "zone of avoidance" would make sense if all of the spiral nebulae were outside the Galaxy and all those lying toward the disk of the Milky Way were obscured.
      3. Curtis also noted that the spectra of the spiral nebulae were inconsistent with spectra of nebulae, but consistent with a large collection of stars.

  6. Hubble's Law

    Hubble's Law for the expansion of space between the galaxies is simply v = Hod. Where v is the apparent recessional velocity of a galaxy, Ho is the Hubble constant, and d is the distance of the galaxy.
    1. We observe galaxies in the Fornax cluster and measure their spectra. We recognize the familiar lines of hydrogen, only they are redshifted. We find that the average redshift for the cluster is 0.45%. At what velocity is the cluster receeding from us in units of km/s?

      The formula for Doppler shift tells us that / = v/c. So,

      v/c = 0.45% = 0.0045

      thus, v = 0.0045c = 0.0045 x 3 x 105km/s

      v = 1,350 km/s

    2. A cepheid variable star is observed within a galaxy in Fornax. Compared to a cepheid observed in the Large Magellanic Cloud (LMC), at 60 kpc distance, this cepheid has the same period and is measured to be 90,000 times fainter. What is the distance to the Fornax cluster in Mpc (1 Mpc = 1 million parsecs)?

      If the two cepheids have the same period then they have the same luminosity. Therefore the difference in their brightnesses is due to their differences in distances. Since b 1/d2,

      bLMC / bFornax = (dFornax/dLMC)2 = 90,000

      dFornax2 = (9 x 104)·(60 x 103pc)2 = 3.24 x 1014pc2

      dFornax = 1.8 x 107pc = 18 Mpc

    3. With this information calculate the value of Ho in units of (km/s)/Mpc.

      v = Hod. So,

      Ho = v/d = 1,350 km/s / 18 Mpc = 75 km/s/Mpc

    4. Now we look to another galaxy far, far away. We measure a redshift for that galaxy as 10%. What is its distance?

      Again, if / = v/c = 10% = 0.1, then v = 0.1c, and

      v = 0.1 x 3 x 105km/s = 3 x 104km/s.
      Also, Ho = 75 km/s/Mpc as just computed. So,

      d = v/ Ho = (3 x 104km/s) / (75 km/s/Mpc)

      d = 400 Mpc

    5. If a star in our own Milky Way Galaxy is measured to have a redshifted spectrum, can the redshift be used with Hubble's law to determine the distance to that star?

      No, Hubble's law is only valid on the large scales where the space between the galaxies is expanding. Locally, like within the Galaxy, gravity is holding everything together and the expansion of space is not observable. So redshifts measured for stars within the Galaxy only tell you about the speed at which that star is moving away, and nothing else.

  7. Stella's Radio Sauce

    Dr. Luxatstuphen aims a collection of powerful telescopes at a very distant QSR.

    1. Detail what she will observe - size, shape, color, spectrum, brightness, etc. In short, what does a faraway QSR look like to the astronomer?

      2. The quasar will appear as a point source in any kind of telescope. In an optical telescope the source will look like an ordinary star within our own Galaxy with about the same brightness, but the spectrum will be different. In radio telescopes the quasar will be very bright, which is quite unusual for stars. The spectrum of the quasar will be observed as an emission spectrum over some continuum. In the spectrum common lines produced by hydrogen will be seen very redshifted. If Dr. Luxatstuphen uses the Hubble Space Telescope and uses fancy-shmancy computer programs to remove the central brightness of the quasar the fuzziness of a galaxy can be seen surrounding the quasar.

    2. Just what is a Quasar? How do they shine?

      3. A quasar appears to be the result of a supermassive black hole sitting at the center of a galaxy consuming large amounts of matter. The black hole itself of course does not shine, but what does is an accretion disk of material spiraling into the black hole and jets of material squirting out from the center of the disk. This material shines essentially by converting its gravitational potential energy into other forms, like heating from viscous friction in the disk.

    3. Compare QSRs to Active and Radio galaxies.

      4. Active galaxies and Radio galaxies are believed to result from the same phenomenon of a supermassive black hole in the centers of a galaxy with an accretion disk of matter falling into the black hole. Active galaxies seem to be black holes that have consumed most of the gas and whatnot in the centers and now are much less brilliant and spectacular. Radio Galaxies are similar to quasar systems that are still quite active, active enough to produce jets that are visible to us by virtue of their orientation. Both active and radio galaxies are seen in the nearby universe, not as far as the quasars.

    4. Why are there no Quasars nearby?

      5. Remember that seeing something at great distances also means seeing them at times long ago. So if all the quasars are far away then that means they existed long ago and not any more. This makes sense if you think about the process of accretion onto the black holes. Eventually, the black holes will have consumed all of the material in their vicinity and there will no longer be an accretion disk as brilliant or active as in the past. Now, it is possible that during galaxy mergers material could get suddenly dumped onto such a dormant black hole and re-ignite a new quasar. So there being no quasars nearby, and hence now in time, is simply because the food supply for the black holes has diminished.

    Luxatstuphen passes her data on to her graduate assistant (Wurxenslaven) for analysis. The QSR has spectral features parked all the way out at 600 nm which ordinarily lie at 120 nm in the laboratory.

    1. What is this Quasar's Redshift?

      2. Redshift, which astronomers usually call z, is given as: z = /.

      Thus, z = (600nm - 120nm)/ 120nm = 480/120

      z = 4

    2. Compare the type of radiation emitted at the original wavelength to kind of telescope will we need to detect it.

      The spectral features were originally emitted in the ultraviolet portion of the elctromagnetic spectrum but will now need to be observed with an optical telescope.

  8. Gravitational Lenses

    1. Provide an example of an observational phenomenon attributed to gravitational lensing.

      There are the multiple images of quasars seen very near each other and having identical spectra, they come in pairs and crosses. There are a few radio Einstein rings observed. There are the galaxy arcs which are the images of background galaxies being lensed by a foreground cluster of galaxies.

    2. Describe the basics of how gravitational lensing works.

      Gravity bends light. If you have a distant source of light and a foreground distribution of matter that light will be bent as it passes through the gravitational field associated with that distribution. The bending of the light leads to more light reaching your line of sight than would have normally. The geometry of the alignment of the source and the foreground matter, as well as the distribution of the matter itself, will lead to various kinds of multiple images being formed of the source. A perfect alignment will yield a ring, called the Einstein ring. If the bending of the light is so small that the multiple images cannot be resolved by a telescope then the source will simply be seen magnified in intensity (microlensing).

    3. Explain how and what gravitational lensing tells us about dark matter.

      Gravitational lensing tells us again that there is dark matter present in clusters of galaxies and how much is there. We can see background objects lensed by foreground clusters, such as galaxies spread into arcs. Using general relativity we can calculate how much matter must be present to account for the lensing. We find that the amount of matter implied by lensing is much greater than the amount seen. There must be dark matter present in those clusters. Thus, using another theory and another observational method, we again find dark matter. This strengthens the argument that it is not a problem in our understanding of gravity but rather real matter that is present.

  9. Olber's Paradox

    Let's see whether or not we can convince ourselves that Obler's paradox really is a paradox. We know that the apparent brightness of a star is inversely proportional to the square of its distance.
    1. Argue that the angular radius of a star is inversely proportional to its distance.

      The parallax formula, d = 1/p, is all you need to show this. If we re-define the parallax angle as the angular radius of a resolved star (like Betelgeuse) then p = . Then just rewrite the above equation:

      = 1/d

    2. For circles on the sky with small angular radius, , the angular area is simply A = 2. Thus, in what quantitative manner does the angular area of a star depend on distance?

      A = 2 = (1/d)2

      A = /d2

    3. Hence, does the apparent brightness per unit angular area depend on the distance to a star?

      Brightness per unit angular area is given by b/A. We know that b = L/(42d2).

      Thus, b/A = L/(42d2) / /d2

      b/A = L/43

      So b/A is independent of distance!!!

    4. Suppose the Universe is homogeneous, infinite in extent, and infinitely old. Argue that every line of sight should intersect a star, making the night (and day!) sky blindingly bright. Thus, at least one of our assumptions must be wrong.

      If the Universe is homogeneous, then everywhere in the Universe, at a time equivalent to today, there will be a certain density of stars, similar to what we observe in our local region of the Universe today. If, in addition, the Universe is infinite in extent and time (into the past), then every line of sight we have will eventually hit a star. From part (c) the apparent brightness per unit angular area is independent of distance, and so the sky will have an apparent brightness per unit angular area as bright as the surface of a star... and we will all be fried!

    5. For which of our assumptions is there strong evidence to the contrary?

      The evidence supporting the Big Bang theory (Cosmic Microwave Background, etc.) suggest that the Universe is not infinitely old. It still could be homogeneous and infinite in extent.

  10. The Fate of the Universe

    What are the geometries and fates of the Universe if the average density of the Universe...
    1. is below the critical density?

      If the average density of the Universe is below the critical density, then the Universe is said to be open. In this case space has negative curvature such that an infinite number of lines drawn through any two points can be parallel, the sum of the angles in a triangle is less than 180°, and the volume of a sphere of radius, r, is greater than 4r3/3. The fate of such a Universe is to expand forever and never stop. This Universe eventually becomes cold, dark, and contains nothing but leptons (electrons, neutrinos, etc.). This Universe can be infinite in space but has a beginning.

    2. is exactly equal to the critical density?

      If the average density of the Universe is exactly equal to the critical density, then the Universe is said to be flat. In this case space has zero curvature such that only two lines drawn through any two points can be parallel, the sum of the angles in a triangle is equal to 180°, and the volume of a sphere of radius, r, is equal to 4r3/3. The fate of such a Universe is to expand forever and stop at time equal to infinity. This Universe also eventually becomes cold, dark, and contains nothing but leptons (electrons, neutrinos, etc.). This Universe is again infinite in space but has a beginning.

    3. exceeds the critical density?

      If the average density of the Universe exceeds the critical density, then the Universe is said to be closed. In this case space has positive curvature such that no two lines are parallel, the sum of the angles in a triangle is greater than 180°, and the volume of a sphere of radius, r, is less than 4r3/3. The fate of such a Universe is to collapse back in on itself in a ``Big Crunch.'' This Universe is finite in both space and time. In the closed case, as in all cases, the spatial and temporal properties of the Universe are intimately related.

  11. The Big Bang Theory

    1. Why is the fact that quasars are found only at high redshifts bad for the Steady State theory of the Universe?

      Quasars are only found at high redshift, and high redshift means a long time ago and far, far away. This means that things are either different where they are, or that things were different in the past. Since we usually take the humble view that we're not somewhere special, the most plausible explanation is that the whole Universe was different in the past. This is contrary to the idea in a steady state Universe that the Universe is the same at all times and at all places.

    2. Why do we expect the Universe to be filled with microwave radiation if the Universe began as a hot Big Bang?

      If the Universe came from a hot big bang, then things must have been really hot in the past. Since anything hot radiates an amount proportional to temperature to the fourth power (blackbody radiation), this means that the Universe must have been radiating like a fiery goat in the past. That radiation, highly redshifted, should be (and is!) visible today.

  12. Hubble Time

    The "Hubble Time" is the age of the Universe calculated by ignoring the effects of gravity.
    1. For a Hubble constant of 50 km/s/Mpc, calculate the Hubble time. (Hint: Take 1/Ho, and simplify units of time remain.)

      There are roughly 3.1 x 1019km in one Mpc, since (3.1 x 1018cm/pc)(106pc/Mpc) = 3.1 x 1024cm/Mpc = 3.1 x 1019km/Mpc.

      Thus the Hubble time, tH, is

      tH = 1/Ho = 1/(50 km/s/Mpc) =

      (3.1 x 1019km/Mpc)/ (50 km/s/Mpc) = 6.2 x 1017s

      There are about 31.6 million seconds/year, so we have tH = 19.6 x 109years =

      19.6 billion years

    2. Now calculate the Hubble time if Ho = 80 km/s/Mpc.

      Since the Hubble time is proportional to 1/Ho, a bigger value of Ho will give a smaller Hubble time. The ratio of times is given by the inverse of the ratio of Hubble constants. Thus, with Ho = 80 km/s/Mpc, we get a Hubble time of (50/80) x 19.6 billion years, or 12.3 billion years.

    3. Compare your results with the derived ages of the oldest globular clusters, 14 billion years. Are there any inconsistencies? (Some recent studies indicate that the globular clusters might be actually only 11-12 billion years old, however)

      If the oldest globular clusters have ages of 14 billion years, they are older than the Universe if Ho = 80 km/s/Mpc. This cannot be, and so there is an inconsistency. Things look better if the Hubble constant is smaller --- say 50 or 60 km/s/Mpc. The inconsistency is much smaller (or nonexistent) if the globular clusters are younger (say, only 11--12 billion years old, as some astronomers claim from new data taken with the Hipparcos satellite).

    4. Suppose the expansion of the Universe is gradually slowing down due to the gravitational attraction of all galaxies to all other galaxies. Explain why the age of the Universe is actually even less than the values calculated in parts a) and b).

      If the expansion of the Universe is slowing down due to gravity, then in the past the expansion must have been proceeding at a faster rate. Thus, looking back in time, with gravity operating, less time must have elapsed from the time everything was infinitely compressed (the Big Bang), than with the first case where we ignored gravity. This implies that in a Universe in which gravity is important on global scales, the actual age of the Universe is less than the value calculated in parts (a) and (b), increasing the potential conflict with globular cluster ages.

Return to Main Homework Page