Homework #4: Solutions

Homework #4: Solutions

  1. What seems to be the problem officer?

    You are driving and inadvertently run a red traffic light and a police officer pulls you over. You decide to tell the officer that you thought the light was green. You explain the Doppler shift of light to the officer and how since you were moving toward the traffic light the wavelengths of light were getting blueshifted. How fast would you have to have been driving for this to be true? Give your answer in both km/s and miles/hr. Should the officer give you a ticket?

    (NOTE: use the wavelength of the red light to be 7000 Å and that of green light to be 5000 Å)

    The Doppler shift formula is /0 = v/c. = 5000 Å - 7000 Å = - 2000 Å (the minus sign indicates a blueshift). So,

    /0 = 2000Å/7000Å = 0.29
    (I've dropped the minus sign, because we know we are talking about a blueshift now.)

    v/c = 0.29 ---> v = 0.29c
    v = 0.29(3x105 km/s) = 8.6 x 104 km/s

    8.6 x 104 km/s * 0.6214 miles/km * 3600 s/hr = 1.9 x 108 miles/hr = 190 million miles per hour !!!

    Yes, you should definitely get a ticket, for speeding!

  2. E = mc-who?

    1. Using Einstein's famous equation E = mc2, show that when 4 protons fuse into 1 helium nucleus via the proton-proton cycle, about 4.14 x 10-12 Joules of energy is released. (The mass of one individual proton is about 1.6725 x 10-27kg; the mass of one helium nucleus is about 6.644 x 10-27 kg.)

      The difference in the masses of the Helium nucleus and the 4 protons is 4.6 x10-29kg.

      (4 x 1.6725 x 10-27kg) - 6.644 x 10-27kg = 4.6 x10-29kg

      E = (4.6 x10-29kg)x( 9.0x1016 m2/s2) = 4.14x10-12 Joules

      (recall one Joule is a kgm2/s2)

    2. The total luminosity (energy radiated per second) of the sun is about 3.85 x 1026 J/s. How many nuclei of helium are being created per second?

      The number of He nuclei produced each second corresponds to the number of fusion reactions occuring (as each reaction produces one He nucleus). Divide the energy output of the Sun by the energy of one fusion reaction to find out how many reactions per second are required to power it, and we'll have our Helium count as well.

      (3.85x1026 J/s)/(4.14x10-12 J/reaction) = 9.29 x1037 reactions (Helium nuclei)/s.

    3. What percentage of the hydrogen mass is converted into energy via fusion?

      The proportional change in mass is the actual change 4.6x10-29kg (note that we can write it as .046 x10-27 kg so that it more easily cancels), divided by the original mass of 4x1.6725x10-27kg = 6.690 x10-27kg.

      (.046 x10-27kg)/(6.690 x10-27kg) = 0.0068

      which expressed as a percentage is 0.68 % ( 0.7 % for those of us who round)

    4. How much mass in the Sun is being converted into energy every second?

      We can solve this by dividing the given Luminosity by c2(A) or by multiplying the values we calculated for reactions per second and mass-loss per reaction (B). Either approach gives us 4.27x109kg.

      (A)

      E/c2 = m

      (3.85 x 1026J)/(9.0 x 1016m2/s2) = 4.27x109kg

      (B)

      (Mass converted/reaction)x(# of reactions/sec) = Mass converted/sec

      (4.6x10-29kg)x(9.29 x1037 reactions/sec) = 4.27x109kg/s

    5. The Sun has a mass of 1.989 x 1030kg. Only 10% of that mass is available for hydrogen fusion in the core. Show that the Sun's lifetime on the main-sequence (how long it burns hydrogen in the core) is 10 Billion years.

      The Hydrogen fusion reaction only converts 0.68% of the reaction mass into energy, so the Sun is actually "using" a tiny fraction of that 10 percent. The total converted will be (0.1x0.0068) = 6.8x10-4 times its total mass

      6.8x10-4 x 1.989 x 1030kg = 1.35x1027kg

      (by E = mc2 this is a total of 1.21x1044 Joules produced!). .

      Since we know both the mass consumption rate and the energy production per second, we can determine the Sun's lifetime with either by dividing mass or energy rates.

      (1.35x1027kg)/(4.27x109kg/s) = 3.15 x 1017sec

      or

      (1.21x1044J)/(3.85 x 1026J/s) = 3.15 x 1017sec

      As there are about 3.15x107 seconds in a year the Sun has 1x1010 - or 10 Billion years to cook.

  3. This star won't be telling its life story to Barbara Walters

    Suppose Putrix is a main sequence star twice as massive as the Sun.

    1. What is Putrix's luminosity relative to the Sun?

      The luminosity of stars on the main sequence is related to their mass by the proportionality, L M4. So we need only set up a ratio to see how luminous Putrix is.

      LP/L = (MP/M)4 = 24
      Therefore
      LP = 16L

    2. If Putrix and the Sun each use about 0.1M of gas as thermonuclear fuel during their main sequence lives, and if the Sun's main sequence life is 10 billion years, what is Putrix's lifetime?

      Luminosity is the amount of energy per second being given off by each star. It is therefore the rate at which energy is used up by the star. Since Putrix is 16 times more luminous that means that it is burning its fuel 16 times faster than the Sun. Since they have the same amount of fuel to burn (0.1M) then Putrix will run out of fuel 16 times faster than the Sun.

      1x1010 years/16 = 6.25 x 108 yrs

      We can mathematically represent this reasoning in the following way. Luminosity is energy per time so L ~ E/, where E is the total amount of energy emitted by the star over its main sequence lifetime, and is the main sequence lifetime. The amount of energy emitted will be equal to the amount of energy produced by fusion of hydrogen to helium over that lifetime. E = mc2. Here m is the amount of matter that was converted into energy. As in the previous problem, 10% of the Sun's mass is available to undergo fusion, and 0.7% of that is converted into energy. So m = 0.007 x 0.1M. The same will hold for Putrix. So we can make a ratio

      L/LP = (E/)*(P/EP)
      Since both the Sun and Putrix burn the same amount of fuel, EP = E, and we have
      L/LP = P/
      Hence,
      P = (L/LP) = (1/16) = 6.25 x 108 yrs

    3. Actually, Putrix will burn the same fraction of gas (10%) as the Sun during its main sequence lifetime. (The Sun burns about 0.1M, 10% of its mass.) So, how may solar masses of gas will Putrix burn?

      Putrix has twice the mass of the Sun but will burn the same fraction of its mass (10%). So it will burn twice as much hydrogen as the Sun will.

      0.1 x MP = 0.1 x 2M = 0.2M

    4. Knowing this, revise your answer to part (b) accordingly to calculate Putrix's main-sequence lifetime.

      Since Putrix has twice as much fuel to burn as the Sun it will take it twice as long as the previous calculation. It also means that Putrix will release twice as much energy as the Sun will over its lifetime. So by the mathematical reasoning in part (b) EP = 2E and thus

      L/LP = (1/2)P/
      P = 2(L/LP) = (2/16) = 1.25 x 109 yrs

  4. H-R Diagrams

    Let us assume that main sequence O, B, A, F, G, K, and M stars live approximately 3 million, 20 million, 300 million, 2 billion, 10 billion, 50 billion, and 200 billion years respectively. Draw and label completely a rough H-R diagram for clusters of stars with ages
    1. 2 million years old


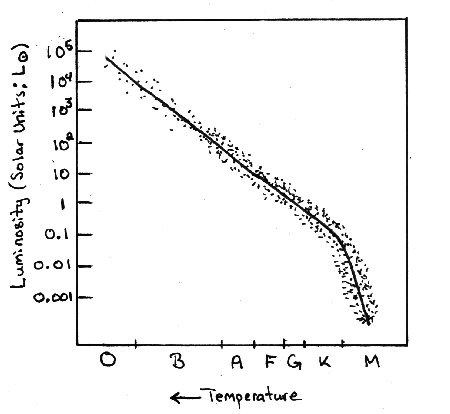
      When the cluster is only 2 million years old none of the stars are yet old enough to have left the Main Sequence. So there should be a full main sequence stretching fom M stars to O stars. Since no stars have left the main sequence yet, there should be no Red Giants or White Dwarfs.

    2. 300 million years old


      When a cluster has reached the age of 300 million years A stars are now running out of hydrogen in their cores and turning into Red Giants. All stars more massive than they (O and B) stars have long since turned into Red Giants and died as type II supernovae. The some of the A stars that are now turning into Red Giants are not massive enough to go supernova and will instead puff off their outer envelopes and end up as White Dwarfs. Remember that stars below 4M will turn into White Dwarfs. The A stars run from about 10 to 100 times the Luminosity of the Sun and since the Luminosity is proportional to mass to the fourth power that means the masses of the A stars are about 2M to 3.2M. So there should be a small population of White Dwarfs as well as a considerable Red Giant population visible.

    3. 10 billion years old


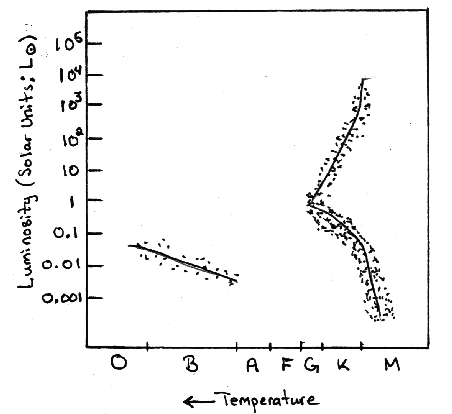
      When a cluster reaches 10 billion years old stars that are like the Sun begin to leave the main sequence and turn into Red Giants. There are no stars on the main sequence above it as they have all died as either supernovas or as Planetary Nebulae into White Dwarfs. Thus the main sequence terminates at the position of the Sun and there is a considerable Red Giant and White Dwarf population.

  5. They might be Red Giants

    Red Giants have proceeded further in the evolutionary sequence than main sequence stars, but is it correct to say that all red giants are older than all main sequence stars? (For example, which star is older, the Sun or a red giant of 10M ?)

    Not all red giants are older than all main-sequence stars. Massive stars, born relatively recently, quickly evolve into red giants, while we know the Sun has been a main-sequence star for the last 5 billion years. As an example, a red giant of 10M could not be a very old star. Stars born with 10M will have luminosities of 104L and thus consume their main-sequence fuel 104/10 = 103 times faster than the Sun. Since the Sun's main-sequence lifetime is 1010 years, the 10M star's lifetime will only be about 107 years. The red-giant phase is even shorter than the main-sequence phase --- say, 2 million years in this example. Thus, the 10M red giant has been a star for only about 12 million years. Compare that to the 5 billion years of the Sun's happy time on the main sequence.

  6. When Stars Explode

    Describe the two main types of supernovae, in terms of both their observed characteristics and their probable explosion mechanisms.

    Type I supernovae are observed to have no hydrogen lines visible in their spectra. They are seen in all kinds of galaxies. They arise when a white dwarf star is accreting matter from a binary companion which is overflowing its Roche lobe. If the white dwarf mass exceeds 1.4M (the Chandrasekhar limit), the star can no longer be supported by electron degeneracy pressure. It starts to collapse and a runaway chain of nuclear reactions occurs. Lower mass nuclei, such as carbon and oxygen, are fused into heavier ones, such as nickel and iron. A vast amount of energy is released which causes the star to explode and leave no remnant star. Material, enriched with heavy elements, is flung into space.

    Type II supernovae are observed to have hydrogen lines visible in their spectra. They are seen primarily in the arms of spiral galaxies (where young stars live). These kinds of supernovae are the endpoint of evolution for very massive stars (M > 10M). After the helium fusion process ends in the cores of these stars they have enough mass to ignite carbon fusion and fusion of heavier elements. An onion layered effect of fusion shells fusing different elements builds up in the interior of the star. The fusion process stops at iron; fusion of iron does not yield more energy than is put into it. An iron core builds up. When the core reaches a mass greater than 1.4M it collapses under gravity and becomes a neutron star, forcing the electrons of atoms into the nuclei and combining with protons to become neutrons and releasing neutrinos. The envelope of the star falls down upon the neutron star and rebounds off in an enormous explosion. Most of the energy released is in the form of neutrinos. Heavy elements, including some heavier than iron, are created during the explosion and flung out into interstellar space.

  7. Black Holes Suck

    1. If the Sun (1M = 2x1030 kg) were a black hole, its Schwarzchild radius (Rs = 2GM/c2) would be only 3 km. What would the Schwarzchild radius be for the following objects?
      1. An 80 kg person

        Once again these calculations are best done with ratios. We'll write the Schwarzchild radius of the object we seek as Rs,? = 2GM?/c2. For the Sun let's write Rs, = 2GM/c2 = 3 km. Now take the ratio:

        Rs,?/Rs, = (2GM?/c2)*(c2/2GM) = M?/M
        And so
        Rs,? = (M?/M)Rs, = (M?/M)*(3 km)

        For an 80 kg person,

        Rs,person = (80 kg/2 x 1030 kg)*3 x 103 m = 1.2 x 10-25 m

      2. Earth (M = 6x1024 kg)

        Rs, = (6x1024 kg/2 x 1030 kg)*3 x 103 m = 9 x 10-3 m = 9 mm

      3. A supermassive black hole with a billion times the mass of the Sun.

        Rs,BH = (1 x 109)*3 x 103 m = 3 x 1012 m = 20 A.U.

    2. How would the orbit of the Earth change if our Sun suddenly collapsed into a black hole? (Assume the mass stays the same.)

      It wouldn't. The elements of the equation that describes the force of gravity between the Earth and the black-hole-sun (F = GMSME/R2) haven't changed! Of course, temperatures here would drop appreciably, so we'd all die horrible deaths, but .. at least we'd be in the same orbit.

    3. Now, a space-goat herder, named Bob, keeps watch over his space-goats by making them wear collars with blue lights that flash in 10 second time intervals. One day one of his flock wanders too close to a black hole and begins to fall toward it. Describe what the fall toward the black hole will look like from Bob's perspective far away from the black hole. Also describe what the fall is like for the poor space-goat.

      From Bob's perspective: Bob will see the space-goat's blue light begin to gravitationally redshift and its color will turn from blue to green to red to infrared, etc. until it (and the space-goat) are no longer visible to any detectors Bob can build. Also, Bob will see the interval of the flashes from the light grow longer and longer as time starts running slower for the space-goat as seen by Bob. Bob would see the space-goat falling slower and slower toward the event horizon of the black hole. He would have to wait forever, however to see the space-goat cross the event horizon.

      From the space-goat's perspective, nothing particular seems strange to him. He will feel tidally stretched out by the Black Hole. When he looks out toward Bob however he will see the light from Bob blueshift and he well see Bob's time run faster than his own.

    4. Nothing that falls beneath the surface of a black hole ever emerges, not even light. So how, then, do astronomers go about trying to detect black holes?

      Black holes themselves may be invisible, but their intense gravity tends to have dramatic effects on their neighborhood. For instance, if a black hole is a member of a binary star system, it will cause its partner to move (much as it did when it was a 'normal' star) - and the doppler shifts produced by that motion can be detected. If you see a star wobbling as if it had a several-solar-mass companion - and you don't see any such companion, chances are you've found a black hole!

      Black holes also can acquire accretion disks of rapidly orbiting infalling matter. The material in these disks becomes intensely hot due to friction as it spirals into the black hole, causing it to glow brightly. So, a disk of rapidly orbiting, very hot matter is another signature of a black hole's presence. These have been observed very clearly at the hearts of some galaxies.

  8. Pair-o-Ducks

    Howard the duck and Donald Duck are in separate space ships initially at rest with respect to one another. Howard leaves for home heading away from Donald at 1/2 the speed of light.
    1. What is Donald's velocity as measured by Howard?

      1/2 the speed of light (away)

    2. Does Donald find that his own meter stick is longer, shorter or equal to 1 meter? Explain.

      Donald sees his meter stick as equal to one meter - his meter stick is not moving away at relativistic velocities. Another way of thinking on the issue: the meter stick is in his little neighborhood of spacetime and so naturally appears normal in all respects. Relativistic changes in perception only crop up between moving observers. Each one sees his piece of space and time as if it were the most perfectly normal place in the universe (assuming there is enough Prozac available).

    3. Does Howard find that his own meter stick is longer, shorter or equal to 1 meter? Explain.

      The same observation just made above applies here. Howard sees Howard meter stick as one meter. It's right there with him.

    4. Does Howard find that Donald's meter stick is longer shorter or equal to 1 meter? Explain.

      Howard thinks that Donald's meter stick is shorter. From Howard's perspective, Donald is zipping away from him; and moving objects (from your perspective) appear to contract in length along their direction of motion.

    5. Does Donald find that Howard's meter stick is longer, shorter or equal to 1 meter? Explain.

      Donald thinks Howard's meter stick is shorter, by the same reasoning.

    6. Does Donald find his watch running faster, slower or the same to Howard's? Explain.

      Donald thinks Howard's watch runs more slowly (i.e. his own runs faster). From your perspective, the moving clock runs slower. Time is dilated.

    7. Does Howard find his watch is running faster, slower or the same as Donald's? Explain.

      Howard thinks Donald's watch runs more slowly (i.e. his own runs faster), for exactly the same reasons. Both Observers Must See the Same Things

    8. Howard and Donald were actually twins. If Howard turns around and meets up with Donald again, who will be older? This is the famous "pair-o-ducks paradox".

      Donald will be the older. When Howard turned around his frame of reference became distinguishable from Donald's (he experienced an acceleration, Donald did not). During his trip he sees the distance between them contract and it seems to him that the round trip takes less time than it should have. Hence he ages less than Donald does.

Return to Main Homework Page