Numbers Big and Small
(11 points)Let's get a little practice using scientific notation and converting units. (Refer to pg. 544 of your text for conversions between metric and English units.)
- Write the number 238,793.387 in scientific notation with only 3 significant digits.
To write this number in scientific notation we need to figure out how many spaces to move the decimal point to the left until we have only one digit to the left of the decimal point. Each space we move the decimal is one power of ten. So to obtain the number 2.38793387 we needed to move the decimal 5 times, or 5 powers of 10. This number to 3 significant digits is 2.39. We round the third digit up or down accordingly. So finally, the answer is:
2.39 x 105 - Write the number 5.765 x 10-7 as a normal string of digits.
In the first problem you can see that multiplying by a positive power of ten indicates how many decimal places to the right one must move the decimal point to obtain a normal string of digits (we went to the left to get the scientific notation, it's opposite the direction to go to obtain the normal string). So multiplying by a negative power of ten moves the decimal to the left by that power. And so we have
0.0000005765 - What is (6 x 104)/(3 x 10-6)? Do not use a calculator. Show your work. What's the name of this number (i.e., how many million, billion, trillion, etc. is this)?
First off 6/3 = 2. That's easy enough. So now we are left with 104/10-6. Use the rules of multiplication and division of exponents. When dividing you subtract the exponents. So 4 - (-6) = 4 + 6 = 10. Thus the answer is
2 x 1010
or 20 x 109 = 20 Billion - A light-year is the distance light travels in one year. If light travels at a speed of 186,000 miles/second how many miles are there in a light-year? How many meters is this? Give all answers in scientific notation and show all work.
Let us remember the relationship between speed, distance, and time.
distance = speed x time (1) In this problem we want to know the distance. We know the speed, and the time is 1 year. But the speed is not given in years, so we need to convert it into seconds. How many seconds are there in one year?60 seconds/minute x 60 minutes/hour x 24 hours/day x 365.26 days/year = 3.16 x 107 seconds/year So now we plug this value into equation (1) with the speed of light givendistance = (1.86 x 105 miles/second) x (3.16 x 107 seconds) = 5.88 x 1012 miles = 5.88 Trillion miles Now, to find out how many meters this is we need only do some unit conversions. From page 544 in the text you find that 1 km = 0.6214 miles and you know that there are 103 m/km. So we have(5.88 x 1012 miles) x (1 km/0.6214 miles) x (103 m/km) = 9.46 x 1015 m = 9.46 Quadrillion meters
Scale Models
(16 points)Suppose you wish to construct a scale model of the Universe. The Sun has an actual diameter of about 1.5 x 106 km, and you represent it by a dot the size of a period (0.5 mm in diameter). The average distance between stars in our region of the Milky Way Galaxy is about 5 light-years. (1 light-year = 9.5 x 1012 km)
- What is the average distance between stars on the scale of your drawing? (Hint: use ratios, and keep track of your units!
The whole point of this problem is to use ratios to get a sense of scale of space and time in the Universe. There's only one piece of math here and that's the ratio. In this scale model the Sun's diameter is 0.5 mm, let's put the numbers in meters for ease (0.5 mm x 1 m/103mm = 5 x 10-4 m). The Sun's actual size is (1.5 x 106 km) x (103 m/km) = 1.5 x 109 m. So our ratio is:
ratio = scale/actual = (5 x 10-4 m)/(1.5 x 109 m) = 3.33 x 10-13 So, in all the following calculations we will just multiply this number by the actual size to get the scale model size.For this part, the actual average distance between stars is about 5 light-years = 5 light-years x (9.5 x 1012 km/light-year) = 4.75 x 1013 km. So let's multiply it by our ratio to find out what it is in the scale model.
scale size = ratio x actual = (3.33 x 10-13) x (4.75 x 1013 km) = 1.58 x 101 km = 15.8 km Think about it, if the Sun were the size of a period located in Berkeley, the nearest star would be in San Francisco!
- The Galaxy is about 105 light-years in diameter. How large is this on your scale?
Let's put this number in km again. 105 light-years x (9.5 x 1012 km/light-year) = 9.5 x 1017 km. Now multiply by the ratio.
scale size = ratio x actual = (3.33 x 10-13) x (9.5 x 1017 km) = 3.16 x 105 km That's just a little less than the average distance between the Earth and the Moon!
- On this same scale, what is the distance to the Andromeda galaxy, about 2 million light-years away? (This is the nearest large galaxy.)
Again, put the number in km. 2 x 106 light-years x (9.5 x 1012 km/light-year) = 1.9 x 1019 km. Now multiply by the ratio.
scale size = ratio x actual = (3.33 x 10-13) x (1.9 x 1019 km) = 6.3 x 106 km - On this same scale, what is the distance to the most distant objects we have seen (quasars and very distant galaxies), about 13 billion light-years away?
13 x 109 light-years x (9.5 x 1012 km/light-year) = 1.2 x 1023 km. Now, multiply by the ratio.
scale size = ratio x actual = (3.33 x 10-13) x (1.2 x 1023 km) = 4.1 x 1010 km = 41 Billion kilometers - Compare your scaled answer in part (d) with the true diameter of the Solar System (as defined by Pluto's orbit), about 12 billion km. Which is larger, and by roughly what factor?
Since the scale is 41 Billion kilometers from the Sun to the most distant reaches it is clearly bigger than the diameter of Pluto's orbit (12 Billion km). The factor by which it is bigger is just
(41 billion km)/(12 billion km) = 3.4 times Now the distance to the farthest reaches is actually a radius not a diameter and so to do this completely correct you must compare the diameter of the scale model Universe (2 x 41 billion = 82 billion) to the diameter of Pluto's orbit. So that's(82 billion km)/(12 billion km) = 6.8 times Either answer will get you full credit.
This will be the same as above but with a different ratio. Let's put both times in seconds so that we can properly compare them.
4.6 x 109 years x (3.16 x 107 seconds/year) = 1.45 x 1017 seconds
- How many seconds ago did the USA achieve independence (1776 A.D.)?
This event occurred 2000 - 1776 = 224 years ago. Let's put that in seconds. It's 224 years x (3.16 x 107 seconds/year) = 7.08 x 109 seconds ago. Now multiply by the ratio:
scaled time = ratio x actual time = (5.96 x 10-13) x 7.08 x 109 seconds ago = 4.2 x 10-3 seconds ago - How long ago did Rome fall (around 476 A.D.)?
This occurred 2000 - 476 = 1,524 years ago. Put that in seconds: 1.524 x 103 years x (3.16 x 107 seconds/year) = 4.82 x 1010 seconds. Now multiply by the ratio...
scaled time = ratio x actual time = (5.96 x 10-13) x 4.82 x 1010 seconds = 2.87 x 10-2 seconds ago - How long ago was the first city, Jericho, built (about 10,000 years ago)?
104 years ago x (3.16 x 107 seconds/year) = 3.16 x 1011 seconds. Now multiply by the ratio...
scaled time = ratio x actual time = (5.96 x 10-13) x (3.16 x 1011 seconds) = 0.188 seconds ago - How long ago did the first modern Homo Sapiens show up in the fossil record (about 100,000 years ago)?
105 years ago x (3.16 x 107 seconds/year) = 3.16 x 1012 seconds. Now multiply by the ratio...
scaled time = ratio x actual time = (5.96 x 10-13) x (3.16 x 1012 seconds) = 1.88 seconds ago - How long ago did the Dinosaurs go extinct (65 Million years ago)?
65 x 106 years ago x (3.16 x 107 seconds/year) = 2.05 x 1015 seconds. Now multiply by the ratio...
scaled time = ratio x actual time = (5.96 x 10-13) x (2.05 x 1015 seconds) = 1.224 x 103 seconds ago
1.224 x 103 seconds x (1 minute/60 seconds) = 20.4 minutes ago - How long ago did the first plants appear on dry land (250 Million years ago)?
250 x 106 years ago x (3.16 x 107 seconds/year) = 7.9 x 1015 seconds. Now multiply by the ratio...
scaled time = ratio x actual time = (5.96 x 10-13) x (7.9 x 1015 seconds) = 4.71 x 103 seconds ago
4.71 x 103 seconds x (1 minute/60 seconds) x (1 hour/60 minutes) = 1.3 hours ago - How long ago was the origin of life on Earth (about 3.8 Billion years ago)?
3.8 x 109 years ago x (3.16 x 107 seconds/year) = 1.2 x 1017 seconds. Now multiply by the ratio...
scaled time = ratio x actual time = (5.96 x 10-13) x (1.2 x 1017 seconds) = 7.16 x 104 seconds ago
7.16 x 104 seconds x (1 minute/60 seconds) x (1 hour/60 minutes) = 19.9 hours ago
How Far is the Horizon?
(13 points)As we discussed in class the horizon is the place where the Earth meets the sky, and the horizon is farther away the higher you get above the surface of Earth. The mean radius of Earth (sea-level) is 6,371 km.
- Let's say you are standing on a small (10-foot) boat out in the ocean. Your feet are essentially at sea-level. Estimate or measure the height of your eyes above your feet while standing. Calculate the distance to the horizon.
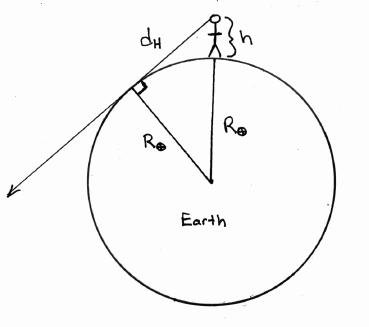
In class I drew a figure similar to the one above and showed you that to do this calculation you needed only to recognize that the horizon is where your line of sight runs tangent to Earth's surface. This is of course a line that is perpendicular to the radius of the Earth, R , and thus we can identify a right triangle with legs, dH (the distance we seek), and R
, and thus we can identify a right triangle with legs, dH (the distance we seek), and R . Also the triangle has a hypotenuse equal to the sum of the Earth's radius and your height above it, h. Using the Pythagorean theorem for right triangles we may then write
. Also the triangle has a hypotenuse equal to the sum of the Earth's radius and your height above it, h. Using the Pythagorean theorem for right triangles we may then write
dH2 + R Solving for the the distance to the horizon, dH, gives 2 = (R
2 = (R + h)2
+ h)2 dH2 = (R With that figured out all you need to do now is just plug and chug... For this first part I'll use my height and chose h = 6 ft. We need to convert that into km to be useful in the calculation. So here goes. + h)2 - R
+ h)2 - R 2
2
or
dH = SQRT[(R + h)2 - R
+ h)2 - R 2]
2]
6 ft x (1 mile/5280 ft) x (1 km/ 0.6214 miles) = 1.83 x 10-3 km Plugging awaydH = SQRT[(6,371 km + 1.83 x 10-3 km)2 - (6,371 km)2]
dH = 4.8 km x (0.6214 miles/km) = 3.0 miles - Now you hike up to Volmer peak (elevation 1,913 ft). Neglecting your own height, how far away is the horizon?
For this part h = 1,913 ft x (1 mile/5280 ft) x (1 km/ 0.6214 miles) = 0.583 km, and thus we have
dH = SQRT[(6,371 km + 0.583 km)2 - (6,371 km)2]
dH = 86.2 km x (0.6214 miles/km) = 53.6 miles - Finally, you are flying out east to see a friend. During the flight the captain tells you that you are flying at a height of 35,000 ft. A young child is sitting in the window seat next to you looking out and wondering how far she can see from way up here. What's the answer?
For this part h = 35,000 ft x (1 mile/5280 ft) x (1 km/ 0.6214 miles) = 10.7 km, and thus we have
dH = SQRT[(6,371 km + 10.7 km)2 - (6,371 km)2]
dH = 369 km x (0.6214 miles/km) = 229 miles
National Lampoon's: Vacation on the Moon
(12 points)Let's say that you took a trip to the Moon. After checking in to your hotel room you walk out onto your balcony to check out the view. It's rather spectacular. Earth is up in the Southwest sky and it's a waxing gibbous, nearly full.
- You want to call your friends back in Berkeley on Earth to tell them about the awesome view. What phase will they see the Moon to be in?
Recall from class that we discussed how the Earth appears from the Moon. In that discussion I told you that Earth exhibited phases as seen from the Moon. That could be readily seen during the demonstration with the globe and the lamp. Also, recall that I told you that the phases were exactly opposite the ones people on Earth would be seeing for the Moon. When the Moon is New, Earth is Full, etc.. So, if you see Earth to be a waxing gibbous from your window, then the Moon is a waning crescent. Think about it. If the Earth is a waxing gibbous then that means it will soon be full. If it will soon be full then the Moon must be viewing it from the position in its orbit where it is between the Earth and Sun. That is when Earth will see the Moon as New. The phase just previous to New is the waning crescent.
- The phone company will only allow you to make the call when the Moon is directly overhead in the location you are calling on Earth. What general time of day will that be in Berkeley? (i.e. noon, midnight, dawn, dusk, or sometime between those)
Since the Moon is a waning crescent it is between 90° and 0° West of the Sun as seen from Earth (Berkeley included). Thus it rises after midnight and before sunrise. It is therefore overhead in the morning sometime before noon and after sunrise.
- You're kinda tired and would like to take a nap, but the Earth is pretty darn bright and is shining a lot of light into the room. You have difficulty sleeping with that much light in the room. How long will you have to wait until Earth sets over the horizon?
Forever! Recall in class how I explained that the Moon always presents the same face to Earth. It spins only once per orbit about the Earth. Its solar day is the same as the synodic month. That means that if you are in a location where the Earth is in the sky, it is always there! It never rises, sets, or moves at all. The only change it goes through is the phases. So pull the shades if you want that nap.
Eclipse
(11 points)- During an annular eclipse of the Sun, the observer sees a ring (Latin annulus) of light, which is the rim of the Sun's photosphere. In other words, the Moon's angular size isn't quite as large as that of the Sun, so one gets a special kind of partial eclipse. When in Earth's elliptical orbit around the Sun and the Moon's elliptical orbit around Earth would this phenomenon reach an extreme (i.e., Sun's angular size is as large as it gets at the same time the Moon's angular size is as small as it gets)? Explain.
Since the orbits are elliptical there are times when the Moon is at it's closest approach to Earth (perigee) and places where it is farthest from Earth (apogee). In these places the Moon is at its largest and smallest apparent angular sizes, respectively. Likewise the Earth's orbit brings it to a point of closest approach (perihelion) and farthest distance (aphelion). In these places the Sun is at its largest and smallest apparent angular sizes, respectively. The angular size changes in an inverse way with distance: smaller the greater the distance, bigger the smaller the distance. So when the Moon is far enough away in its orbit that its angular size is less than that of the Sun we get an annular eclipse. This is most extreme if the eclipse were to occur when the Moon was at apogee and Earth at perihelion. (NOTE: you need not have mentioned the words apogee and perihelion specifically)
- When people in New York see a total lunar eclipse, what type of eclipse do people one-fourth of the way around Earth see? (Assume that the Moon is visible in both skies.)
They will also see a total lunar eclipse. This is true for two reasons. One is that since it's stated that the Moon is visible in both skies at the same time both places are seeing the same Moon and they will both see it completely covered by Earth's shadow. This was mentioned specifically in class. Secondly, since Earth's shadow is huge it takes the Moon longer than 12 hours to move all the way through it. Thus everyone on Earth will be able to witness at least part of the eclipse, but not the total eclipse (that only lasts for a maximum of 1 hour 40 minutes).
Where in the World is Gilligan?
(11 points)In a forgotten episode of Gilligan's Island the Professor finds a magical goat that can communicate via radio signals. They use the goat to make contact with civilization. They are saved! But first they must give someone their coordinates so that they can be found. Not much survived the Minnow's demise, but they do have a watch that is still running on Pacific Standard Time. Plus they have a sextant and can measure angles in the sky with high accuracy.
- First they wait for nightfall and locate the Big Dipper and use the pointer stars Merak and Dubhe to locate Polaris. They know that Polaris is about 1° from the North Celestial Pole (I should say the professor knows that, the magical goat might also). They measure the angle of the North Celestial Pole above the horizon to be 28°. What is their latitude?
As mentioned numerous times in class, the angle of Polaris above the horizon is equal to your latitude. Take a look at the following figure:

In the figure, angle l is your latitude and angle p is the angle above the horizon that the North Celestial Pole makes. l + b = 90° also l + a = 90° and a + p = 90° as well. Putting those three equations together tells you that l = p. So Gilligan and company are at a latitude of 28° North. - On the next day they wait for the Sun to cross the local meridian, this happens at 3:04 PM PST, by their watch. Recall that Pacific Standard Time is the Mean Solar Time at a longitude of 120° West of the Prime Meridian. What is their longitude?
For this calculation you need to recall that the Sun moves about the sky, covering 360° every 24 hours, or 15°/hr. Also recall that at a time of 12:00 noon PST the Sun is crossing the meridian as seen from the longitude of 120° West. Since the Sun does not cross Gilligan's meridian until 3 hours later that means that the Sun was East of the meridian at noon and hence they are West of 120° West Longitude. Since it was 3:04 PM when the Sun transited for them then they are
3.0667 hrs x 15°/hr = 46° West of 120° West Longitude in other words they are located at166° West Longitude
Hey Baby, What's Your Sign?
(12 points)As we discussed in class the Sun signs of Astrology are out of date. The precession of Earth's axis has altered the constellation that the Sun is in during any given month. Additionally, the International Astronomical Union recognizes 13 constellations in the Zodiac.
- Using an online star map generator, or the planetarium software provided with your text or in class, determine what constellation the Sun was in at the time of your birth. Is this the same as the Sun sign given for you in the newspaper (check out any newspaper and site the source)?
If you took note of your actual sign when I put up the overheads in class that's fine as well. Some of you may have found that you still had the same sign whereas others would have shifted over one sign. For example, My birthdate is September 18th, 1973. That put me just at the cusp of Virgo in the old astrologers' horoscopes and just at the other cusp in the modern constellation recognized by astronomers. But I remain a Virgo.
- Read the Horoscope of your real Sun sign from at least three different newspapers or websites. If you are an Ophiuchus (Nov. 30th - Dec. 17) just read the one for the date of your birth printed in the paper (either Sagittarius or Scorpius). Make a copy of the three horoscopes and turn them in. How well do they agree? Do they actually make any predictions? If so, did they come true?
You will likely have found that the predictions did not agree well, at times even being contradictory. Most of these so-called predictions were also likely just advice and not a prediction at all. Any predictions that were made were likely so vague as to have any interpretation to make them appear accurate in retrospect.
Here is one example of a horoscope for Virgo on Tuesday, May 30th:
VIRGO
(Aug. 23 -Sept. 22)
Tackling major household projects could be your main area of focus today as things have been put off for as long as you, or the spouse. are willing to put up with. even though you are as industrious as the busiest beaver don't forget to take some time out to rest during the heat of the day.Well that was not true at all since I didn't spend much of that day at home, and the last bit is just advice not a prediction.
Here's another for 05/30/2000:
Actions speak louder than words, so get busy. Don't wait for approval--go ahead even if the light's red.Hmmm, I don't even know what that's supposed to mean. Certainly didn't apply to anything I did that day.
Here's one last horoscope from the New York Post for 5/30/2000:
VIRGO (Aug. 24-Sept. 23): Some think your ambitions are too lofty. Some think you are aiming too high. But according to the planets, you have what it takes to reach the top and stay there. Don't listen to those who counsel caution, because caution never got anyone anywhere. Take a few risks - they will pay off.That pretty much can apply to anyone doing anything. It's basically just advice. Not really a prediction.
Going Retro
(14 points)- In words and in pictures show how both Ptolemy's model of the Universe and Copernicus' model of the Universe explained the retrograde motion of the planets.
In Ptolemy's model the planets are attached to circles that are attached to circles that both rotate at the same time, the larger one is rotating about the Earth. This causes a real loop-the-loop motion in space that would appear as retrograde motion to observes on Earth. See figure 3.

In Copernicus' model the planets (including Earth) all revolve about the Sun in perfect circles. The retrograde motion is just an illusion of perspective when one planet is "lapped" by another. See figure 4
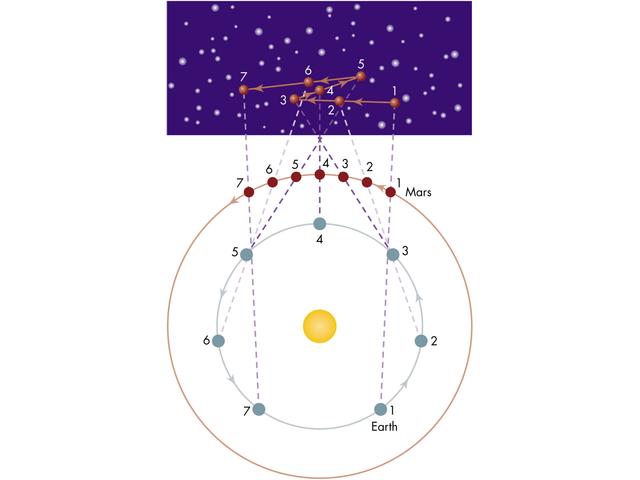
- In Copernicus' time measurements of the Planets' positions were not sufficient to be able to differentiate one model from the other as being more accurate. Explain why, using modern scientific reasoning, we would have to go with Copernicus' model as the best explanation of nature if we lived then.
In modern scientific research we use a philosophy called Occam's razor. It states that when presented with two hypotheses that explain and predict a phenomenon equally well, we should go with the more simple. There's absolutely no reason why we should prefer the more complex explanation if the simpler does just as well at explaining it. Thus when it was seen that Copernicus' model did just as well at predicting the positions of the planets we should have chosen it for its simplicity, even though it went against our most fundamental beliefs and prejudices.