Homework #5

Homework #5

This assignment is not due for credit. It is for you to attempt on your own and use to study for the final exam. Attempt each problem before looking at the solutions.

  1. Sunsets are Red, the Sky is Blue...

    "White light," emitted by the Sun, and other G-type stars, is a mixture of all colors with equal intensities.
    1. When you look up into the sky, why does the part away from the Sun look blue?
    2. Why does the Sun look red at sunset? What happens to the blue light?
    3. In what ways are your above answers analogous to the explanations for the bluish color of reflection nebulae and the process of interstellar reddening?

  2. There's More Than Nougat in the Milky Way

    1. Draw a edge-on-view diagram of our Galaxy. Label all of the following: disk, halo, bulge, globular clusters, open clusters, and the location of the Sun.
    2. How do we know the location of the Sun within our Galaxy?

  3. Stellar Populations and Spiral Structure

    1. In terms of stellar populations, why do spiral arms tend to be bluer than the rest of the Galaxy?
    2. If a type II supernova were to occur in our Galaxy, would you expect it to occur within a spiral arm, or outside of a spiral arm? Why?
    3. Why do we not believe that the spiral arms are material spiral arms?
    4. What do we believe is the cause of spiral structure in our Galaxy?

  4. Beware of the Dark Side

    The expression for the mass of the Milky Way Galaxy within a distance, r, from the center is M = v2r/G, where G is Newton's gravitational constant (numerically equal to 4.30 x 10-6(kpc/M)·(km/s)2) and v is the orbital speed of a star at distance r. This formula works equally well for other spiral galaxies. Thus, the mass of a galaxy as a function of radial distance from the center can be obtained from the rotation curve of the galaxy.

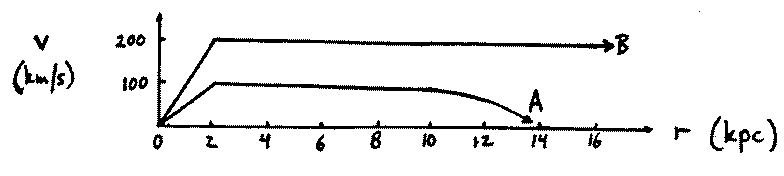
    1. Shown above are two possible rotation curves of the Milky Way Galaxy. (Niether one is necessarily correct.) If rotation curve B is correct, what is the mass of the Milky Way Galaxy within a radius of 10kpc? (Keep careful track of units, and express your answer in solar masses.)
    2. Compared with rotation curve B, does rotation curve A yield a larger, or smaller, mass for the Milky Way Galaxy within a radius of 8kpc? By What factor?
    3. Suppose rotation curve B is correct. If the luminous material (stars, gas) in the Milky Way Galaxy extends out to a radius of 14Kpc, and becomes quite faint beyond that, what must be true at radii larger than 14kpc?

  5. It May Be A Small World, But It's A Big Universe

    It is now known that our Galaxy is one of billions in a truly gargantuan Universe. But this was only discovered in the 1920s.
    1. Why did Harlow Shapley think that the "spiral nebulae" were contained within the Milky Way Galaxy, and that the Milky Way Galaxy was the entire extent of the Universe?
    2. Why did Heber Curtis think that the "spiral nebulae" were actually "island universes"?

  6. Hubble's Law

    Hubble's Law for the expansion of space between the galaxies is simply v = Hod. Where v is the apparent recessional velocity of a galaxy, Ho is the Hubble constant, and d is the distance of the galaxy.
    1. We observe galaxies in the Fornax cluster and measure their spectra. We recognize the familiar lines of hydrogen, only they are redshifted. We find that the average redshift for the cluster is 0.45%. At what velocity is the cluster receeding from us in units of km/s?
    2. A cepheid variable star is observed within a galaxy in Fornax. Compared to a cepheid observed in the Large Magellanic Cloud (LMC), at 60 kpc distance, this cepheid has the same period and is measured to be 90,000 times fainter. What is the distance to the Fornax cluster in Mpc (1 Mpc = 1 million parsecs)?
    3. With this information calculate the value of Ho in units of (km/s)/Mpc.
    4. Now we look to another galaxy far, far away. We measure a redshift for that galaxy as 10%. What is its distance?
    5. If a star in our own Milky Way Galaxy is measured to have a redshifted spectrum, can the redshift be used with Hubble's law to determine the distance to that star?

  7. Stella's Radio Sauce

    Dr. Luxatstuphen aims a collection of powerful telescopes at a very distant QSR.

    1. Detail what she will observe - size, shape, color, spectrum, brightness, etc. In short, what does a faraway QSR look like to the astronomer?
    2. Just what is a Quasar? How do they shine?
    3. Compare QSRs to Active and Radio galaxies.
    4. Why are there no Quasars nearby?

    Luxatstuphen passes her data on to her graduate assistant (Wurxenslaven) for analysis. The QSR has spectral features parked all the way out at 600 nm which ordinarily lie at 120 nm in the laboratory.

    1. What is this Quasar's Redshift?
    2. Compare the type of radiation emitted at the original wavelength to kind of telescope will we need to detect it.

  8. Gravitational Lenses

    1. Provide an example of an observational phenomenon attributed to gravitational lensing.
    2. Describe the basics of how gravitational lensing works.
    3. Explain how and what gravitational lensing tells us about dark matter.

  9. Olber's Paradox

    Let's see whether or not we can convince ourselves that Obler's paradox really is a paradox. We know that the apparent brightness of a star is inversely proportional to the square of its distance.
    1. Argue that the angular radius of a star is inversely proportional to its distance.
    2. For circles on the sky with small angular radius, , the angular area is simply A = 2. Thus, in what quantitative manner does the angular area of a star depend on distance?
    3. Hence, does the apparent brightness per unit angular area depend on the distance to a star?
    4. Suppose the Universe is homogeneous, infinite in extent, and infinitely old. Argue that every line of sight should intersect a star, making the night (and day!) sky blindingly bright. Thus, at least one of our assumptions must be wrong.
    5. For which of our assumptions is there strong evidence to the contrary?

  10. The Fate of the Universe

    What are the geometries and fates of the Universe if the average density of the Universe...
    1. is below the critical density?
    2. is exactly equal to the critical density?
    3. exceeds the critical density?

  11. The Big Bang Theory

    1. Why is the fact that quasars are found only at high redshifts bad for the Steady State theory of the Universe?
    2. Why do we expect the Universe to be filled with microwave radiation if the Universe began as a hot Big Bang?

  12. Hubble Time

    The "Hubble Time" is the age of the Universe calculated by ignoring the effects of gravity.
    1. For a Hubble constant of 50 km/s/Mpc, calculate the Hubble time. (Hint: Take 1/Ho, and simplify units of time remain.)
    2. Now calculate the Hubble time if Ho = 80 km/s/Mpc.
    3. Compare your results with the derived ages of the oldest globular clusters, 14 billion years. Are there any inconsistencies? (Some recent studies indicate that the globular clusters might be actually only 11-12 billion years old, however)
    4. Suppose the expansion of the Universe is gradually slowing down due to the gravitational attraction of all galaxies to all other galaxies. Explain why the age of the Universe is actually even less than the values calculated in parts a) and b).

Return to Main Homework Page